Vật lý

I. NHỮNG ĐẶC ĐIỂM CỦA DAO ĐỘNG CƠ.

1. Thí nghiệm.

2. Dao động cơ.

- Dao động cơ học: là quá trình chuyển động qua lại quanh một vị trí cân bằng.

- Dao động tuần hoàn: là dao động cơ học mà cứ sau những khoảng thời gian bằng nhau, vật trở lại vị trí cũ theo hướng cũ (trạng thái của vật được lặp lại như cũ). Giai đoạn nhỏ nhất được lặp lại trong dao động tuần hoàn gọi là dao động toàn phần (hay một chu trình).

- Dao động điều hoà: là dao động tuần hoàn đơn giản nhất, trong đó li độ của vật biến đổi theo hàm cosin của thời gian.

- Đặc điểm:

+ Là hình chiếu của chuyển động tròn đều xuống đường thẳng trong mặt phẳng quỹ đạo.

+ Mỗi dao động điều hoà điều hoà được biểu diễn bằng một vectơ quay.

+ Biên độ dao động A phụ thuộc vào cách kích thích ban đầu.

II. DAO ĐỘNG ĐIỀU HÒA.

1. Đồ thị của dao động điều hòa.

Đồ thị của dao động điều hòa là đường biểu diễn vị trí (li độ) của vật theo thời gian. Nó có dạng hình sin.

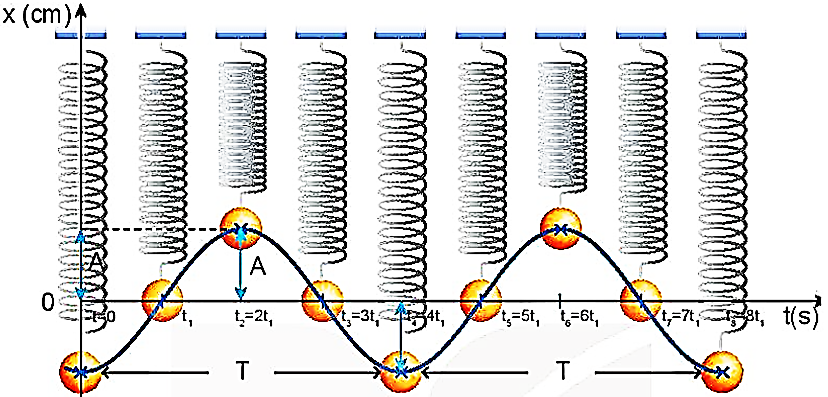
2. Phương trình dao động điều hòa.

Phương trình dao động điều hòa có dạng:

$x=Acos(\omega.t+\varphi)$

trong đó:

x là li độ dao động (cm, m).

A là biên độ dao động (cm, m). Biên độ A là hằng số luôn dương và phụ thuộc cách kích thích dao động.

ω la tần số góc (rad/s). Tần số góc ω là hằng số luôn dương và phụ thuộc đặc điểm cấu tạo của con lắc.

φ là pha ban đầu (rad). Pha ban đầu φ ∈ [-π; π], nó phụ thuộc vào gốc thời gian và chiều dương trục tọa độ.

(ω.t+φ) là pha dao động (rad).

I. CÁC ĐẠI LƯỢNG ĐẶC TRƯNG CỦA DAO ĐỘNG ĐIỀU HÒA.

- Li độ x: là độ dịch chuyển từ vị trí cân bằng đến vị trí của vật tại thời điểm t.

- Biên độ A: là độ dịch chuyển cực đại của vật tính từ vị trí cân bằng.

- Chu kì T: là khoảng thời gian vật thực hiện một dao động. Đơn vị là giây (s).

- Tần số f: là số dao động vật thực hiện được trong một giây. Đơn vị là Héc (Hz) hoặc s^-1.

$f = \frac{1}{T}$

- Tần số góc ω: là góc quét được trong một giây. Đơn vị là radian trên giây (rad/s).

$\omega=2\pi f = \frac{2\pi}{T}$

* Trong dao động điều hòa thì A, T, f, ω là những đại lượng không đổi, không phụ thuộc vào thời điểm quan sát. Với các vật khác nhau thì các đại lượng này khác nhau. Vì thế chúng là những đại lượng đặc trưng cho dao động điều hòa.

II. PHA BAN ĐẦU. ĐỘ LỆCH PHA.

1. Pha ban đầu.

- Pha ban đầu φ cho biết tại thời điểm bắt đầu quan sát, vật dao động điều hòa ở đâu và sẽ đi về phía nào. Nó có giá trị nằm trong đoạn từ -π đến π radian.

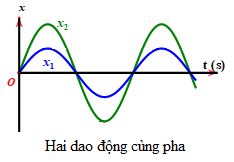
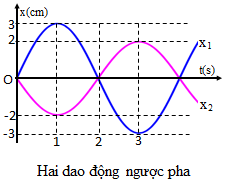
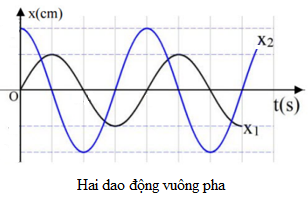
2. Độ lệch pha của hai dao động cùng chu kì.

- Nếu ${\varphi _1} > {\varphi _2}$ thì dao động 1 sẽ sớm pha hơn dao động 2.

- Nếu ${\varphi _1} < {\varphi _2}$ thì dao động 1 sẽ trễ pha hơn dao động 2.

- Nếu ${\varphi _1} = {\varphi _2}$ thì dao động 1 sẽ cùng (đồng) pha với dao động 2.

- Nếu ${\varphi _1} = {\varphi _2} \pm \pi $ thì dao động 1 sẽ ngược pha với dao động 2.

- Nếu ${\varphi _1} = {\varphi _2} \pm \frac{\pi }{2}$ thì dao động 1 sẽ vuông pha với dao động 2.

I. VẬN TỐC CỦA VẬT TRONG DAO ĐỘNG ĐIỀU HÒA.

1. Phương trình của vận tốc.

- Định nghĩa của vận tốc: $v=\frac{\Delta x}{\Delta t}=x'$

thay biểu thức $x=Acos(\omega.t+\varphi)$ vào, ta được biểu thức của vận tốc:

$v=-\omega A sin(\omega t + \varphi )=\omega A cos(\omega t + \varphi +\frac{\pi}{2})$

- Ta thấy vận tốc sớm pha hơn li độ một góc $\frac{\pi}{2}$

- Công thức độc lập thời gian:

$\frac{x^2}{A^2}+\frac{v^2}{\omega^2 A^2}=1$

hay

$v=\pm\omega\sqrt{A^2-x^2}$

- Từ biểu thức độc lập ta thu được các giá trị đặc biệt:

+ Khi x = 0 ⇒ v = ±ωA.

+ Khi x = ±A ⇒ v = 0.

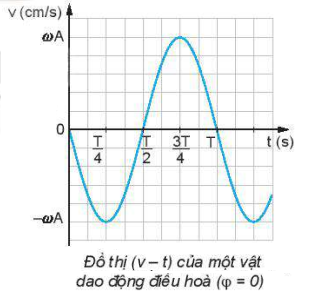
2. Đồ thị của vận tốc.

- Từ biểu thức $v=-\omega Asin(\omega.t+\varphi)$ ta thấy đồ thị của vận tốc theo thời gian cũng là đường hình sin.

II. GIA TỐC CỦA VẬT TRONG DAO ĐỘNG ĐIỀU HÒA.

1. Phương trình của gia tốc.

- Định nghĩa của gia tốc: $a=\frac{\Delta v}{\Delta t}=v'$

thay biểu thức $v=-\omega Asin(\omega.t+\varphi)$ vào, ta được biểu thức của gia tốc:

$a=-\omega^2 A cos(\omega t + \varphi )=\omega^2 A cos(\omega t + \varphi +\pi) = -\omega^2x$

- Ta thấy gia tốc sớm pha hơn vận tốc một góc $\frac{\pi}{2}$ và gia tốc ngược pha với li độ.

- Công thức độc lập thời gian:

$\frac{a^2}{\omega^4 A^2}+\frac{v^2}{\omega^2 A^2}=1$

- Từ biểu thức độc lập ta thu được các giá trị đặc biệt:

+ Khi x = 0 ⇒ a = 0.

+ Khi x = A ⇒ a = -ω²A.

+ Khi x = -A ⇒ a = ω²A.

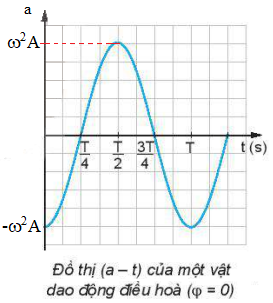
2. Đồ thị của gia tốc.

- Từ biểu thức $a=-\omega^2 Acos(\omega.t+\varphi)$ ta thấy đồ thị của gia tốc theo thời gian cũng là đường hình sin.

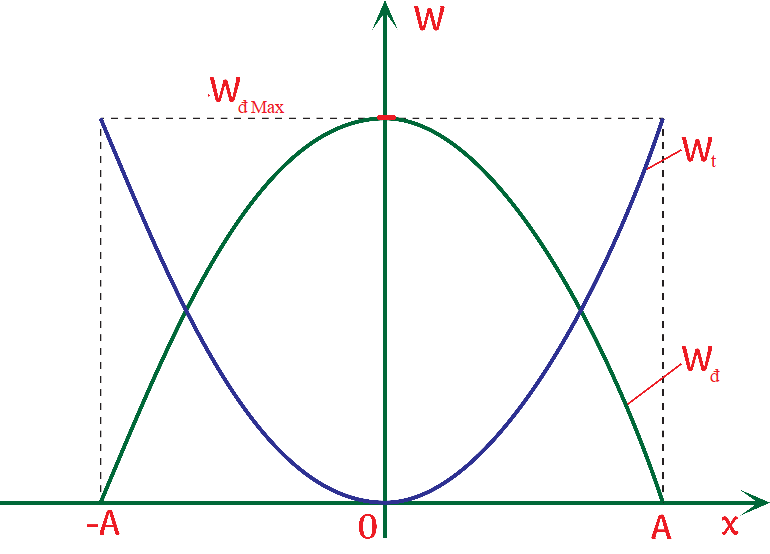
I. ĐỘNG NĂNG.

- Động năng được xác định bởi công thức:

$W_{đ}=\frac{1}{2}mv^2$

thay $v=\pm\omega\sqrt{A^2-x^2}$ vào, ta được biểu thức của động năng:

$W_{đ}=\frac{1}{2}m\omega^2(A^2-x^2)$

- Đây là biểu thức cho thấy sự biến thiên của động năng theo li độ. Đây là hàm bậc 2 theo x với hệ số âm, nên đồ thị của động năng theo li độ là đường parabol có bề lõm hướng xuống.

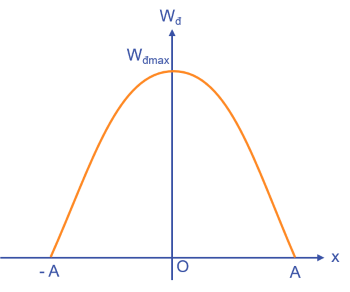
- Động năng có giá trị cực đại $W_{đMax}=\frac{1}{2}m\omega^2A^2$ tại vị trí x=0.

- Động năng có giá trị cực tiểu $W_{đMin}=0$ tại vị trí x=±A.

⇒ Khi vật chuyển động từ biên về vị trí cân bằng thì động năng tăng, và ngược lại.

II. THẾ NĂNG.

- Thế năng được xác định bởi công thức:

$W_{t}=W_{đMax}-W_{đ}$

thay biểu thức $W_{đMax}=\frac{1}{2}m\omega^2A^2$ và $W_{đ}=\frac{1}{2}m\omega^2(A^2-x^2)$ vào, ta được biểu thức của thế năng:

$W_{t}=\frac{1}{2}m\omega^2x^2$

- Đây là biểu thức cho thấy sự biến thiên của thế năng theo li độ. Đây là hàm bậc 2 theo x với hệ số dương, nên đồ thị của thế năng theo li độ là đường parabol có bề lõm hướng lên.

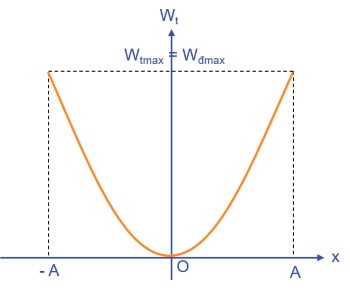
- Thế năng có giá trị cực đại $W_{tMax}=\frac{1}{2}m\omega^2A^2$ tại vị trí x=±A.

- Thế năng có giá trị cực tiểu $W_{tMin}=0$ tại vị trí x = 0.

⇒ Khi vật chuyển động từ biên về vị trí cân bằng thì thế năng giảm, và ngược lại.

III. CƠ NĂNG.

Trong dao động điều hòa, có sự chuyển hóa qua lại giữa động năng và thế năng của vật. Tuy nhiên tổng động năng và thế năng là cơ năng luôn bảo toàn (không đổi).

$W=W_{đ}+W_{t}=\frac{1}{2}m\omega^2A^2$

III. CƠ NĂNG CỦA CON LẮC ĐƠN VÀ CON LẮC LÒ XO.

1. Con lắc lò xo.

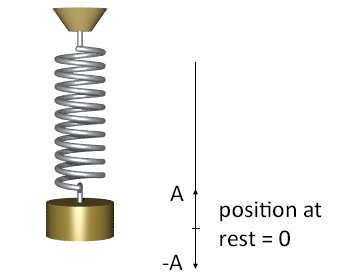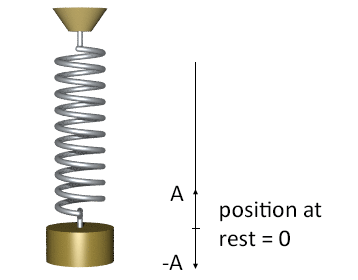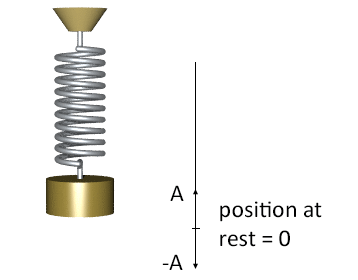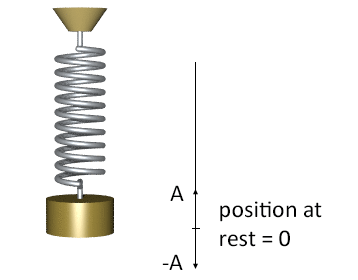
- Khi bỏ qua ma sát thì dao động của con lắc lò xo là dao động điều hòa. Thế năng của con lắc lò xo là thế năng đàn hồi của lò xo khi bị biến dạng. Khi chọn mốc thế năng tại vị trí cân bằng, ta có biểu thức thế năng:

$W_{t}=\frac{1}{2}kx^2$

với k là độ cứng của lò xo, đơn vị (N/m).

- Kết hợp với $W_{t}=\frac{1}{2}m\omega^2x^2$ ta suy ra được:

$\omega=\sqrt{\frac{k}{m}}$

Từ đó suy ra chu kì

$T=2\pi\sqrt{\frac{m}{k}}$

và tần số:

$f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$

- Cơ năng của con lắc lò xo là:

$W=W_{tMax}=\frac{1}{2}kA^2=\frac{1}{2}m\omega^2A^2$

2. Con lắc đơn.

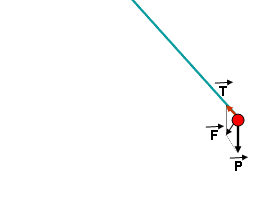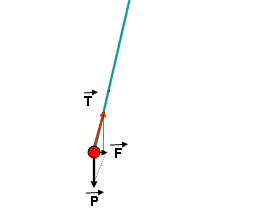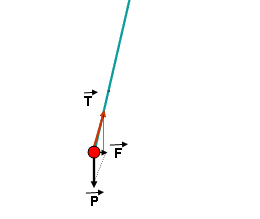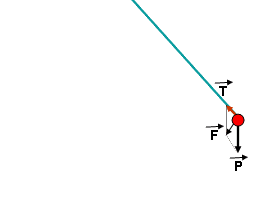
- Khi bỏ qua ma sát thì dao động của con lắc đơn là dao động điều hòa. Thế năng của con lắc đơn là thế năng trọng trường của vật. Khi chọn mốc thế năng tại vị trí cân bằng, ta có biểu thức thế năng:

$W_{t}=mgh$

với h là độ cao của vật so với mốc thế năng. Dễ dàng chứng minh được h = l(1-cosα). Từ đó ta có biểu thức thế năng của con lắc đơn:

$W_{t}=mgl(1-cos{\alpha})$

- Khi góc α ≤ 10⁰ thì thế năng con lắc đơn có thể viết:

$W_{t}=\frac{1}{2}m\omega^2s^2$

với

$\omega=\sqrt{\frac{g}{l}}$

Từ đó suy ra chu kì

$T=2\pi\sqrt{\frac{l}{g}}$

và tần số

$f=\frac{1}{2\pi}\sqrt{\frac{g}{l}}$

- Cơ năng của con lắc đơn là:

$W=W_{tMax}=mgl(1-cos{\alpha_0})=\frac{1}{2}m\omega^2A^2$

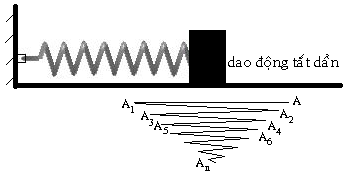
I. DAO ĐỘNG TẮT DẦN.

1. Thí nghiệm.

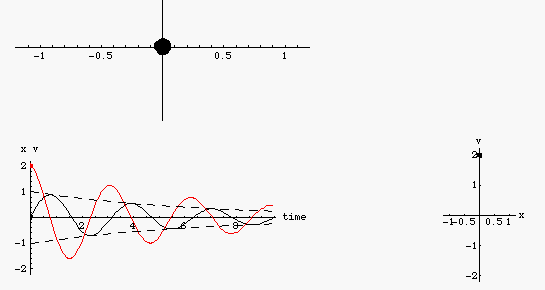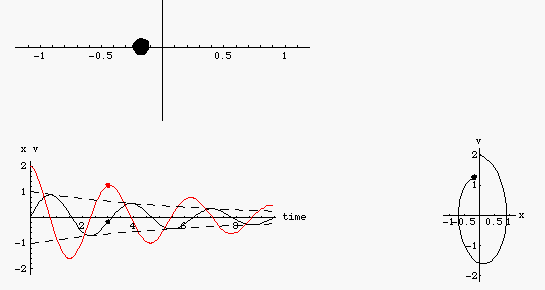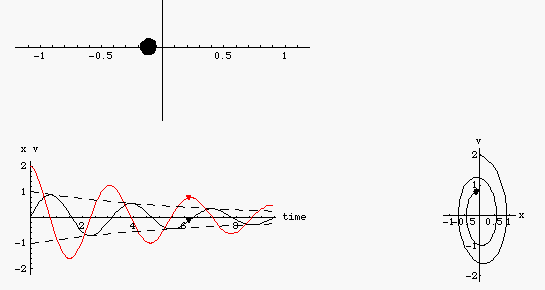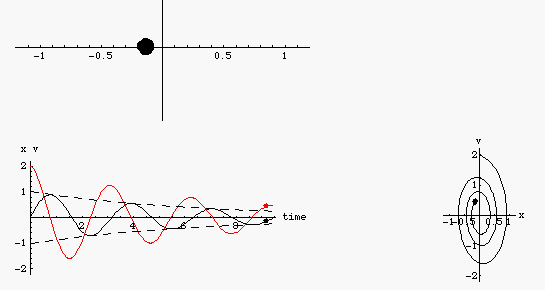
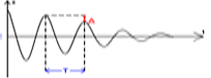
- Dao động tắt dần là dao động có biên độ dao động giảm dần theo thời gian. Nguyên nhân gây ra dao dộng tắt dần là do lực ma sát và lực cản của môi trường.

- Do biên độ giảm dần, do đó đó cơ năng của vật cũng giảm dần. Phần năng lượng mất mát đó chuyển thành năng lượng thắng công cản, nhiệt, hoặc nội năng....

2. Ứng dụng.

- Bộ phận giảm sốc của xe máy, xe ô tô

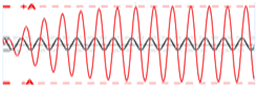
II. DAO ĐỘNG CƯỠNG BỨC.

1. Khái niệm dao động cưỡng bức.

- Dao động cưỡng bức là dao động xảy ra dưới tác dụng của ngoại lực tuần hoàn có tần số f bất kì. Khi dao động ổn định thì tần số của dao động cưỡng bức bằng tần số của ngoại lực.

2. Đặc điểm.

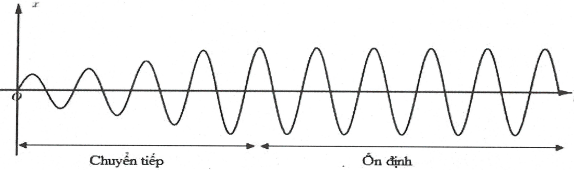
Dao động cưỡng bức khi ổn định có các đặc điểm sau:

- Biên độ của dao động cưỡng bức không đổi và có tần số bằng tần số của lực cưỡng bức.

- Biên độ của dao động cưỡng bức phục thuộc vào biên độ của ngoại lực và độ chênh lệch giữa tần số ngoại lực và tần số riêng của dao động. Khi tần số của lực cưỡng bức càng gần tần số riêng thì biên độ dao động cưỡng bức càng lớn.

III. HIỆN TƯỢNG CỘNG HƯỞNG.

1. Định nghĩa. Hiện tượng cộng hưởng là hiện tượng biên độ của dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của ngoại lực cưỡng bức tiến đến bằng tần số riêng f₀ của dao động.

- Điều kiện để có cộng hưởng là: f=f₀

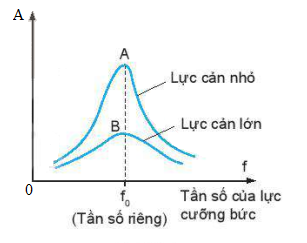
2. Giải thích.

Khi tần số của ngoại lực bằng tần số riêng của dao động, thì hệ được cung cấp năng lượng một cách nhịp nhàng, đúng lúc, do đó biên độc của hệ sẽ tăng dần lên. Biên độ dao động đạt tới giá trị cực đại khi tốc độ tiêu hao năng lượng do ma sát bằng tốc độ cung cấp năng lượng cho hệ.

3. Hiện tượng cộng hưởng trong đời sống.

- Hữu dụng:

+ Hộp đàn guitar, violon: tần số không khí trong hộp đàn phải phù hợp tần số dao động của các dây đàn.

+ Lò vi sóng: tần số vi sóng phải phù hợp tần số dao động của các phân tử nước trong thực phẩm.

- Tác hại: Các công trình xây dựng phải được thiết kế sao cho có tần số riêng tránh bằng các tần số ngoại lực mạnh.

Chuyên đề 1: PHÂN LOẠI DAO ĐỘNG CƠ

	Định nghĩa	Đặc điểm
DAO ĐỘNG CƠ HỌC	- Là quá trình chuyển động qua lại quanh một vị trí cân bằng.	- Là khái niệm tổng quát
DAO ĐỘNG TUẦN HOÀN	- Là dao động cơ học mà cứ sau những khoảng thời gian bằng nhau trạng thái của vật được lặp lại như cũ. Giai đoạn nhỏ nhất được lặp lại trong dao động tuần hoàn gọi là dao động toàn phần (hay một chu trình).	- Là khái niệm tập con của dao động cơ
DAO ĐỘNG ĐIỀU HÒA	Là dao động tuần hoàn đơn giản nhất, trong đó li độ của vật biến đổi theo hàm cosin của thời gian.	- Là hình chiếu của chuyển động tròn đều xuống đường thẳng trong mặt phẳng quỹ đạo. - Mỗi dao động điều hoà điều hoà được biểu diễn bằng một vectơ quay. - Biên độ dao động A phụ thuộc vào cách kích thích ban đầu.
DAO ĐỘNG TỰ DO	Là dao động dưới tác dụng của nội lực.	- Là dao động điều hòa với chu kì riêng T₀ và tần số góc riêng ω₀ - Phụ thuộc đặc điểm cấu tạo của hệ
DAO ĐỘNG TẮT DẦN	Là dao động có biên độ giảm dần theo thời gian do ma sát.	- Không phải là dao động điều hoà. - Phụ thuộc vào biên độ. - Phụ thuộc vào độ nhớt. - Phụ thuộc vào ma sát. * Con lắc lò xo dao động tắt dần với biên độ ban đầu là A và hệ số ma sát là μ. Sau 1 nửa chu kì biên độ còn lại là A₁, sau 2 nữa chu kì biên độ giảm còn A₂, sau 3 nữa chu kì biên độ giảm còn A₃… - Độ giảm biên độ: Theo định luật bảo toàn năng lượng: $ A - {A_1} = {A_1} - {A_2} = {A_2} - {A_3} = {A_3} - {A_4} = ... = \frac{{2\mu mg}}{k} $ + Trong ½ dao động thì biên độ giảm: $ \Delta {A_{\frac{1}{2}}} = \frac{{2\mu mg}}{k} = \frac{{2\mu g}}{{{\omega ^2}}} $;$ \Delta {A_{\frac{1}{2}}} = 2\mu l $ + Trong một dao động thì biên độ giảm: $ \Delta A = \frac{{4\mu mg}}{k} $ - Số lần đi qua vị trí cân bằng: $ n = \frac{A}{{\Delta A}} = \frac{{kA}}{{2\mu mg}} $ + Số dao động thực hiện được: $ m = \frac{n}{2} = \frac{{kA}}{{4\mu mg}} $ - Quãng đường vật đi được: theo định luật bảo toàn cơ năng: $ s = \frac{{k{A^2}}}{{2\mu mg}} $ - Thời gian vật dao động đến lúc dừng lại: $ t = m\bar T $ với $ \bar T $ là thời gian trung bình của 1 dao động tắt dần. - Tỉ lệ phần trăm năng lượng giảm dần: $ \frac{{W - {W_1}}}{W} = 1 - {\left( {\frac{{{A_1}}}{A}} \right)^2} $.
DAO ĐỘNG CƯỠNG BỨC	Là dao động chịu tác dụng của ngoại lực tuần hoàn F=F₀cos(Ωt)	Có hai giai đoạn: - Giai đoạn chuyển tiếp: Biên độ A tăng dần. - Giai đoạn ổn định: + f_CB=f_Lực + ω_CB=ω_Lực= Ω + A∈(F₀, Δf=f_lực-f₀) + Đây là loại dao động điều hòa.
DAO ĐỘNG DUY TRÌ	Là dao động được cung cấp thêm năng lượng để bù trừ năng lượng bị mất do ma sát mà không làm thay đổi tần số riêng.	Ngoại lực được điều khiển sao cho: + f_DT=f₀ + ω_DT=ω₀ + Biên độ A được duy trì như cũ không đổi.
HIỆN TƯỢNG CỘNG HƯỞNG	Là dao động cưỡng bức có biên độ tăng đến giá trị cực đại khi tần số lực cưỡng bức bằng tần số riêng.	- Biên độ A đạt cực đại. Ma sát càng nhỏ thì A càng lớn (cộng hưởng nhọn). + f_CH= f_Lực= f₀ + ω_CH= ω_Lực=Ω= ω₀

Chuyên đề 2: DAO ĐỘNG ĐIỀU HÒA

1. Định nghĩa: Dao động điều hoà là dao động mà li độ của vật biến đổi theo định luật dạng cos (hoặc sin) theo thời gian.

2. Tính chất:

- Là hình chiếu của chuyển động tròn đều xuống đường thẳng trong mặt phẳng quỹ đạo.

- Mỗi dao động điều hoà điều hoà được biểu diễn bằng một vectơ quay.

- Biên độ dao động A phụ thuộc vào cách kích thích ban đầu.

3. Chu kì dao động: là khoảng thời gian thực hiện một dao động toàn phần. Hoặc chu kì là khoảng thời gian ngắn nhất vật trở về trạng thái cũ. Chu kì không phụ thuộc vào cách kích thích dao động, chỉ phụ thuộc vào cấu tạo của hệ.

4. Tần số: là số dao động vật thực hiện được trong một giây.

5. Véctơ quay: Mỗi dao động điều hoà được biểu diễn bằng một véctơ quay $ \overrightarrow {OM} $ có độ dài bằng biên độ A, quay đều quanh điểm O với tốc độ góc ω. Ở thời điểm ban đầu t=0, góc giữa Ox và $ \overrightarrow {OM} $ là φ (pha ban đầu).

5. Phương trình dao động: x=Acos(ωt+φ)

6. Vận tốc tức thời: v=ωAcos(ωt+φ+π/2)

- Vectơ vận tốc $ \overrightarrow v $ cùng chiều chuyển động và đổi chiều tại hai biên.

- Đạt giá trị cực đại khi vật qua vị trí cân bằng theo chiều dương (ωA), giá trị cực tiểu khi vật qua vị trí cân bằng theo chiều âm (-ωA).

- Đạt độ lớn cực đại khi vật ở vị trí cân bằng (ωA), độ lớn cực tiểu ở hai biên (0).

- Đồ thị của vận tốc v theo li độ x và theo gia tốc a là đường elip, theo thời gian t là đường cosin.

7. Gia tốc tức thời: a=ω²Acos(ωt+φ+π)=-ω²x

- Vectơ gia tốc $ \overrightarrow a $ luôn hướng về vị trí cân bằng và đổi chiều tại vị trí cân bằng.

- Có độ lớn tỉ lệ với độ lớn của li độ.

- Đạt giá trị cực đại khi vật ở biên âm (ω²A), giá trị cực tiểu khi vật ở biên dương (-ω²A).

- Đạt độ lớn cực đại khi vật ở hai biên (ω²A), độ lớn cực tiểu ở vị trí cân bằng (0).

- Đồ thị của gia tốc a theo li độ x là đoạn thẳng, theo vận tốc v là đường elip, theo thời gian t là đường cosin.

Liên hệ giữa x và v	Liên hệ giữa x và a	Liên hệ giữa a và v
$ \frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1 $ Hệ thức độc lập	$ a = - {\omega ^2}x $ Phương trình bậc 1	$ \frac{{{a^2}}}{{{\omega ^4}{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1 $ Hệ thức độc lập
Đồ thị (x, v) là đường elip	Đồ thị (x, a) là đoạn thẳng	Đồ thị (a, v) là đường elip
V sớm pha π/2 so với x	a sớm pha π so với x	a sớm pha π/2 so với v

8. Năng lượng:

- Cơ năng: bằng tổng động năng cộng thế năng: $ {W} = \frac{1}{2}m{\omega ^2}{A^2} $.

+ Khi bỏ qua ma sát, cơ năng bảo toàn.

- Thế năng: $ {W_t} = \frac{1}{2}m{\omega ^2}{x^2} $

+ Đạt giá trị cực đại tại hai biên: $ {W_{tMax}} = \frac{1}{2}m{\omega ^2}{A^2} $

+ Đạt giá trị cực tiểu tại vị trí cân bằng: W_t=0

- Động năng: $ {W_đ } = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}({A^2} - {x^2}) $

+ Đạt giá trị cực đại tại vị trí cân bằng: $ {W_{đMax}} = \frac{1}{2}m{\omega ^2}{A^2} $

+ Đạt giá trị cực tiểu tại hai biên: W_đ=0

* Khi W_đ=nW_t thì:

- Li độ: $ x = \pm \frac{A}{{\sqrt {n + 1} }} $

- Vận tốc: $ v = \pm \omega A\sqrt {\frac{n}{{n + 1}}} $

- Gia tốc: $ a = \pm \frac{{\omega ^2}A}{\sqrt {n + 1} } $

* Các tỉ số:

- Động năng chia thế năng: $ \frac{{{W_đ }}}{{Wt}} = \frac{{{A^2}}}{{{x^2}}} - 1 $

- Động năng chia cơ năng: $ \frac{{{W_đ }}}{W} = 1 - \frac{{{x^2}}}{{{A^2}}} $

- Thế năng chia cơ năng: $ \frac{{{W_t}}}{W} = \frac{{{x^2}}}{{{A^2}}} $

* Lưu ý: Dao động điều hoà có tần số góc là ω, tần số f, chu kỳ T. Thì động năng và thế năng biến thiên với tần số góc 2ω, tần số 2f, chu kỳ T/2. Cơ năng không thay đổi.

9. Đồ thị của dao động điều hòa: Đồ thị của dao động điều hòa là đường cosin.

Chuyên đề 3: CON LẮC LÒ XO

I. Cấu tạo con lắc lò xo: Con lắc lò xo gồm một lò xo có độ cứng k, một đầu cố định, một đầu được gắn vào vật nặng khối lượng m.

1. Điều kiện để con lắc lò xo dao động điều hòa:

- Biên độ dao động nằm trong giới hạn đàn hồi.

- Bỏ qua ma sát.

2. Phương trình dao động điều hòa: x=Acos(ωt+φ)

- Phương trình vận tốc: v = ωAcos(ωt+φ+π/2)

+ Vận tốc sớm pha hơn li độ π/2.

- Phương trình gia tốc: a = ω²Acos(ωt+φ+π)

+ Gia tốc sớm pha hơn vận tốc π/2.

+ Gia tốc sớm pha hơn li độ π.

2. Các công thức cơ bản:

- Tần số góc: $ \omega = \sqrt {\frac{k}{m}} $

- Chu kì: $ T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} $

- Tần số: $ f = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} $

- Cơ năng: $ W = \frac{1}{2}k{A^2} $

+ Khi bỏ qua ma sát, cơ năng bảo toàn.

- Thế năng: $ {W_t} = \frac{1}{2}k{x^2} $

+ Đạt giá trị cực đại tại hai biên: $ {W_{tMax}} = \frac{1}{2}k{A^2} $

+ Đạt giá trị cực tiểu tại vị trí cân bằng: W_t=0

- Động năng: $ {W_đ} = \frac{1}{2}m{v^2} = \frac{1}{2}k({A^2} - {x^2}) $

+ Đạt giá trị cực đại tại vị trí cân bằng: $ {W_{tMax}} = \frac{1}{2}k{A^2} $

+ Đạt giá trị cực tiểu tại hai biên: W_t=0

3. Phần công thức mở rộng:

- Điều kiện để hai vật không rời khỏi nhau:

+ Vật m₁ được đặt trên vật m₂ dao động điều hoà theo phương thẳng đứng (Hình 1). Để m₁ luôn nằm yên trên m₂ trong quá trình dao động thì: $ {A_{Max}} = \frac{g}{{{\omega ^2}}} = \frac{{({m_1} + {m_2})g}}{k} $

+ Vật m₁ và m₂ được gắn vào hai đầu lò xo đặt thẳng đứng, m₁ dao động điều hoà (Hình 2). Để m₂ luôn nằm yên trên mặt sàn trong quá trình m₁ dao động thì: $ {A_{Max}} = \frac{{({m_1} + {m_2})g}}{k} $

+ Vật m₁ đặt trên vật m₂ dao động điều hoà theo phương ngang. Hệ số ma sát giữa m₁ và m₂ là µ, bỏ qua ma sát giữa m₂ và mặt sàn (Hình 3). Để m₁ không trượt trên m₂ trong quá trình dao động thì: $ {A_{Max}} = \mu \frac{g}{{{\omega ^2}}} = \mu \frac{{({m_1} + {m_2})g}}{k} $

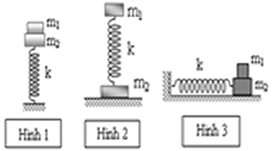
- Cắt lò xo: Một lò xo có độ cứng k và chu kì T, khi được cắt thành n cái lò xo nhỏ giống hệt nhau, thì mỗi lò xo nhỏ có độ cứng k’=nk và chu kì $ T' = \frac{T}{{\sqrt n }} $

- Một lò xo có độ cứng k và chiều dài l được cắt thành các lò xo có độ cứng k₁, k₂, và chiều dài tương ứng là l₁, l₂… thì có: kl = k₁l₁ = k₂l₂ =....= k_nl_n

- Ghép khối lượng: Con lắc lò xo gắn vật nặng m₁ có chu kì T₁ và con lắc lò xo gắn vật nặng m₂ có chu kì T₂.

+ Khi mắc hai vật m₁+m₂ vào lò xo thì chu kì dao động bằng: $ {T^2} = T_1^2 + T_2^2 $

+ Khi mắc vật có khối lượng m=m₁-m₂ vào lò xo thì chu kì dao động bằng: $ {T^2} = \left| {T_1^2 - T_2^2} \right| $

- Ghép lò xo: Con lắc lò xo có độ cứng k₁ có chu kì T₁ và con lắc lò xo có độ cứng k₂ có chu kì T₂.

+ Khi ghép hai lò xo nối tiếp:

. Độ cứng: $ \frac{1}{k} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}} $

. Chu kì: $ {T^2} = T_1^2 + T_2^2 $

+ Khi ghép hai lò xo song song:

. Độ cứng: $ k = k_1 + k_2 $

. Chu kì:$ \frac{1}{{{T^2}}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}} $

4. Phần công thức thêm riêng của con lắc lò xo treo thẳng đứng: Lò xo treo thẳng đứng có chiều dài tự nhiên là l₀, khi mắc vật có khối lượng m và đầu dưới của lò xo và để vật nằm cân bằng, khi đó lò xo giãn một đoạn Δl.

- Độ biến dạng của lò xo thẳng đứng khi vật ở vị trí cân bằng: $ \Delta l = \frac{{mg}}{k} $

- Tần số góc: $ \omega = \sqrt {\frac{{g}}{\Delta l}} $

- Tần số: $ f = \frac{1}{2\pi} \sqrt {\frac{{g}}{\Delta l}} $

- Chu kì: $ T = 2\pi \sqrt {\frac{{\Delta l}}{g}} $

- Chiều dài của lò xo:

+ Trường hợp vật treo ở phía dưới:

. Chiều dài cực tiểu của lò xo (khi vật ở vị trí cao nhất): l_Max= l₀ + Δl - A

. Chiều dài cực đại của lò xo (khi vật ở vị trí thấp nhất): l_Max= l₀ + Δl + A

. Chiều dài lò xo khi vật ở VTCB: l_CB= l₀ + Δl = $ \frac{{{l_{Max}} + {l_{Min}}}}{2} $

+ Trường hợp vật nằm ở phía trên:

. Chiều dài cực tiểu của lò xo (khi vật ở vị trí cao nhất): l_Min = l₀ - Δl - A

. Chiều dài cực đại của lò xo (khi vật ở vị trí thấp nhất): l_Min = l₀ - Δl + A

. Chiều dài lò xo khi vật ở VTCB: l_CB= l₀ - Δl = $ \frac{{{l_{Max}} + {l_{Min}}}}{2} $

- Lực đàn hồi:

+ Là lực đưa vật về vị trí lò xo không biến dạng.

+ Có độ lớn tỉ lệ với độ biến dạng của lò xo.

+ Khi vật treo ở dưới:

+ Với chiều dương hướng xuống thì: F_đh= k|Δl + x|

+ Với chiều dương hướng lên thì: F_đh= k|Δl - x|.

+ Khi vật treo ở trên:

+ Với chiều dương hướng xuống thì: F_đh= k|Δl + x|

+ Với chiều dương hướng lên thì: F_đh= k|Δl - x|.

* Trong trường hợp lò xo nằm trên mặt phẳng nghiêng có góc nghiêng α so với phương ngang thì: $ \Delta l = \frac{{mg.sinα}}{k} $ và chúng ta dùng lại các công thức của lò xo treo thẳng đứng, nhưng thay $ g = g.sinα$

Chuyên đề 4: CON LẮC ĐƠN

I. Cấu tạo con lắc đơn: Con lắc đơn gồm một vật nặng treo vào một sợi dây không giãn, không khối lượng. Vật nặng có kích thước không đáng kể so với chiều dài sợi dây.

1. Điều kiện để con lắc dao động điều hòa:

- Dây treo không giãn, không khối lượng.

- Biên độ dao động nhỏ.

- Bỏ qua ma sát.

2. Phương trình dao động điều hòa:

- Li độ dài: s=S₀cos(ωt+φ)

- Li độ góc: α=α₀cos(ωt+φ)

Trong đó li độ dài và li độ góc liên hệ nhau qua công thức: s=αl và S₀=α₀l

3. Các công thức cơ bản:

- Tần số góc: $ \omega = \sqrt {\frac{g}{l}} $

- Chu kì: $ T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{l}{g}} $

- Tần số: $ f = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} $

- Vận tốc: v²=2gl(cosα-cosα₀).

+ Vận tốc gần đúng (hệ thức độc lập): $ {v^2} = ω^2{(S_0^2 - s^2)}= gl{(α_0^2 - α^2)} $

- Cơ năng: W=mgl(1-cosα₀).

+ Cơ năng gần đúng: W= mω²S₀²= mglα₀²

- Thế năng: W_t=mgl(1-cosα)= mω²s²

+ Đạt giá trị cực đại tại hai biên: W_tMax=mgl(1-cosα₀)

+ Đạt giá trị cực tiểu tại vị trí cân bằng: W_t=0

- Động năng: W_đ=mgl(cosα-cosα₀).

+ Đạt giá trị cực đại tại vị trí cân bằng: W_tMax=mgl(1-cosα₀)

+ Đạt giá trị cực tiểu tại hai biên: W_t=0

II. Phần công thức mở rộng:

1. Ghép con lắc: Con lắc đơn chiều dài l₁ có chu kì T₁ và con lắc đơn chiều dài l₂ có chu kì T₂.

- Khi nối l₁+l₂ tạo thành con lắc đơn có chu kì: $ {T^2} = T_1^2 + T_2^2 $

- Khi nối l₁-l₂ tạo thành con lắc đơn có chu kì: $ {T^2} = T_1^2 + T_2^2 $

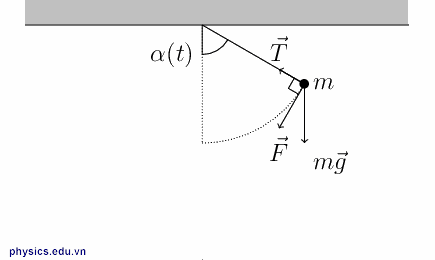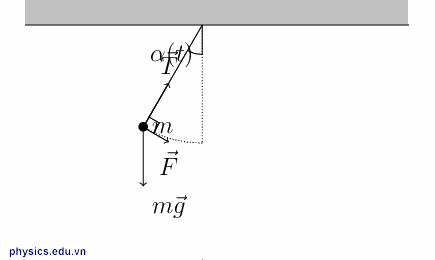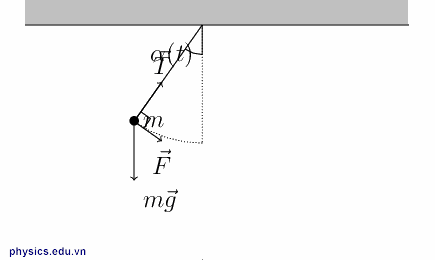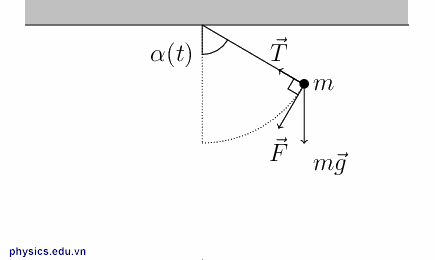
2. Con lắc mắc đinh: Con lắc đơn có chiều dài l dao động điều hòa, trên phương thẳng đứng, người ta đóng một cây đinh, chia chiều dài sợi dây thành hai đoạn l₁ và l₂. Khi đó con lắc sẽ dao động với chu kì: $ T = \frac{{{T_1} + {T_2}}}{2} = \pi \frac{{\sqrt {{l_1}} + \sqrt {{l_2}} }}{{\sqrt g }} $

3. Con lắc đơn dao động trong trọng trường biểu kiến: Khi con lắc đơn chịu tác dụng thêm của lực phụ $ \vec F $, thì hợp của lực phụ $ \vec F $ và trọng lực $ \vec P $ gọi là trọng lực biểu kiến $ \vec P' = \vec P+\vec F$.

- Trọng lực biểu kiến này sinh ra gia tốc trọng trường biểu kiến: $ \vec g' = \vec g+\vec a$

- Do đó chu kì dao động của con lắc bây giờ được xác định bởi: $ T' = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{l}{g'}} $

- Con lắc đơn được treo trên trần thang máy đang đi Lên-Nhanh dần, hoặc đang đi Xuống-Chậm dần. Hoặc quả cầu được tích điện Q > 0 và đặt trong điện trường hướng Xuống, hoặc Q < 0 và hướng Lên. Khi đó ngoại lực cùng chiều với trọng lực $ \vec F \uparrow \uparrow \vec P $ và $ g' = g + \frac{F}{m} $

- Con lắc đơn được treo trên trần thang máy đang đi Lên-Chậm dần, hoặc đang đi Xuống-Nhanh dần. Hoặc quả cầu được tích điện Q>0 và đặt trong điện trường hướng Lên, hoặc Q < 0 và hướng Xuống. Khi đó ngoại lực ngược chiều với trọng lực $ \vec F \uparrow \downarrow \vec P $ và: $ g' = g - \frac{F}{m} $

- Quả cầu được tích điện Q>0 và đặt trong điện trường hướng Ngang hoặc con lắc được treo vào trần chiếc xe đang chạy với gia tốc a theo phương ngang. Khi đó ngoại lực vuông góc với trọng lực $ \vec F $⊥$ \vec P $ và $ g' = \sqrt {{g^2} + {a^2}} $. Và con lắc dao động quanh vị trí cân bằng mới lệch so với phương thẳng đứng 1 góc β với $ \tan \beta = \frac{F}{P} $.

4. Biến thiên của chu kì:

- Biến thiên theo nhiệt độ: Khi thay đổi nhiệt độ thì chiều dài l của con lắc đơn thay đổi: Δl=lαΔt. Từ đó dẫn đến chu kì dao động của con lắc đơn thay đổi $ \frac{{T' - T}}{T} = \frac{\alpha }{2}(t' - t) $.

- Biến theo theo độ cao: Khi đưa con lắc lên độ cao h thì gia tốc trọng trường đổi thành: $ g = G\frac{M}{{{{(R + h)}^2}}} $. Từ đó dẫn đến chu kì dao động của con lắc đơn thay đổi thành $ \frac{T_{Cao} - T}{T} = \frac{h}{R} $.

- Biến theo theo độ sâu: Khi đưa con lắc xuống độ sâu s thì gia tốc trọng trường thay đổi thành $ g = G\frac{M(R-s)}{{{{R }^3}}} $. Từ đó dẫn đến chu kì dao động của con lắc đơn thay đổi $ \frac{T_{Sâu} - T}{T} = \frac{s}{2R} $.

5. Đồng hồ quả lắc: Gọi T là chu kì của đồng hồ chạy đúng, T’ là chu kì con lắc chạy sai. Nếu T’>T thì đồng hồ sẽ chạy chậm (trễ). Nếu T’ < T thì đồng hồ sẽ chạy nhanh (sớm).

- Trong 1 giây đồng hồ thực tế chạy lệch: $ \frac{{\left| {T' - T} \right|}}{T} $ giây.

- Trong 1 ngày lệch: 86400$ \frac{{\left| {T' - T} \right|}}{T} $ giây.

Vật lí Phổ thông

Chuyên trang Trắc nghiệm Trực tuyến

Thiết kế: Ths. Nguyễn Đăng Hân - 09133.90441

Chương 1: Dao động