Vật lý

I. VỊ TRÍ CỦA VẬT CHUYỂN ĐỘNG TẠI CÁC THƠI ĐIỂM.

- Một số khái niệm cơ bản
+ Chuyển động cơ: là sự thay đổi vị trí của vật đó so với các vật khác theo thời gian.
+ Chất điểm: là những vật có kích thước rất nhỏ so với quãng đường đi được hoặc so với khoảng cách mà ta đề cập đến.
+ Quỹ đạo: là đường nối những vị trí liên tiếp của vật theo thời gian trong quá trình chuyển động
- Cách xác định vị trí của một chất điểm:
+ Chọn 1 vật làm mốc O
+ Chọn hệ toạ độ gắn với O
→ Vị trí của vật là toạ độ của vật trong hệ toạ độ trên.

+ Hệ toạ độ 1 trục (sử dụng khi vật chuyển động trên một đường thẳng):	+ Hệ toạ độ 2 trục (sử dụng khi vật chuyển động trên một đường cong trong một mặt phẳng):
Toạ độ của vật ở vị trí M: \(x=\overline {OM} \)	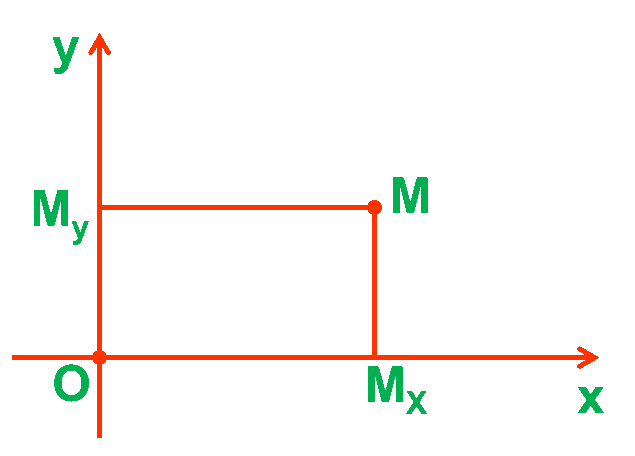Toạ độ của vật ở vị trí M: \(x=\overline {OM_x} \) và \(y=\overline {OM_y} \)

- Cách xác định thời điểm:

. Dùng đồng hồ.
. Chọn một gốc thời gian gắn với đồng hồ trên.
. Thời điểm vật có toạ độ x là khoảng thời gian tính từ gốc thời gian đến khi vật có toạ độ x.
. Lưu ý phân biệt thời điểm và thời gian: Ví dụ: “Bây giờ là 5h45m” là nói về thời điểm, “Cô Nhi Lúng đi từ nhà đến trường mất 15 phút” là nói về thời gian.

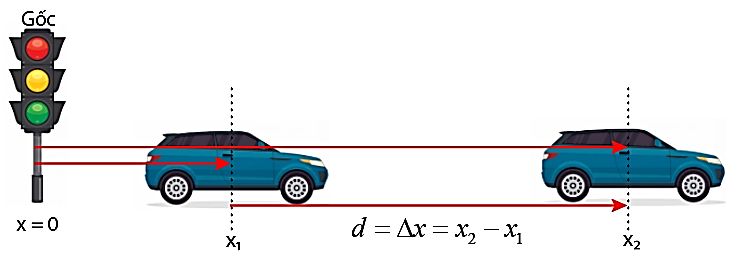
Hệ quy chiếu = Hệ tọa độ gắn với vật mốc + Đồng hồ và gốc thời gian

II. ĐỘ DỊCH CHUYỂN.

- Độ dịch chuyển là một đại lượng vectơ (\(\vec{d}\) có:
+ Điểm đặt (gốc): tại vị trí ban đầu.
+ Phương: là đường thẳng đi qua điểm đầu và điểm cuối.
+ Chiều (hướng): từ vị trí đầu đến vị trí cuối.
+ Độ lớn: bằng khoảng cách giữa vị trí đầu và vị trí cuối.
- Trong chuyển động thẳng véc tơ độ dời nằm trên đường thẳng quỹ đạo.
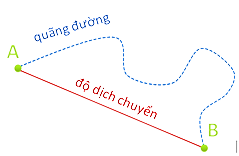
- Khi vật chuyển động thẳng không đổi chiều thì độ lớn độ dịch chuyển và quãng đường đi được bằng nhau. Khi chuyển động thẳng có đổi chiều thì quãng đường đi được và độ dịch chuyển có độ lớn không bằng nhau.

III. PHÂN BIỆT ĐỘ DỊCH CHUYỂN VÀ QUÃNG ĐƯỜNG ĐI ĐƯỢC.

Độ dịch chuyển là 1 đại lượng véc tơ, có thể nhận giá trị dương, âm hoặc bằng 0	Trong khi quãng đường đi được là 1 đại lượng vô hướng, không âm

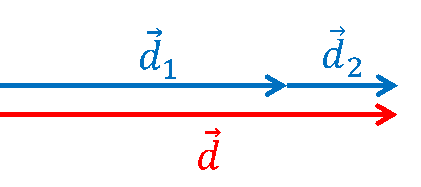
IV. TỔNG HỢP ĐỘ DỊCH CHUYỂN.

Tổng hợp độ dịch chuyển bằng cách tổng hợp vectơ.

\(\vec{d}=\vec{d_1}+\vec{d_2}\)

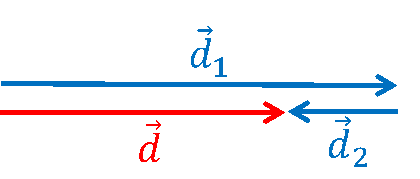
Khi \(\overrightarrow {{d_1}} \nearrow \nearrow \overrightarrow {{d_2}} \) thì: d = d₁ + d₂	Khi \(\overrightarrow {{d_1}} \nearrow \swarrow \overrightarrow {{d_2}} \) thì: d = \|d₁ - d₂\|	Khi \(\overrightarrow {{d_1}} \bot \overrightarrow {{d_2}} \) thì: \(d=\sqrt{d_1^2+d_2^2}\)

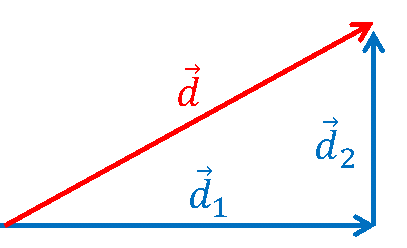
I. TỐC ĐỘ.

Tốc độ là đại lượng đặc trưng cho tính nhanh chậm của chuyển động.

1. Tốc độ trung bình.

- Tốc độ trung bình của vật (kí hiệu là v_tb) được xác định bằng thương số giữa quãng đường vật đi được và thời gian để vật thực hiện quãng đường đó.

\(v=\frac{s}{t}\)

hay

\(v=\frac{\Delta s}{\Delta t}\)

- Đơn vị: m/s, km/h
- Đổi đơn vị: 1 m/s = 3,6 km/h.

2. Tốc độ tức thời.

Tốc độ tức thời là Tốc độ trung bình trong khoảng thời gian rất nhỏ là tốc độ tức thời (kí hiệu v) diễn tả sự nhanh, chậm của chuyển động tại thời điểm đó.

II. VẬN TỐC.

1. Vận tốc trung bình.

- Vận tốc trung bình là đại lượng vecto được xác định bằng thương số giữa độ dịch chuyển của vật và thời gian để vật thực hiện độ dịch chuyển đó.

\(\overrightarrow {{{\rm{v}}_{tb}}} = \frac{{\vec d}}{{\Delta t}} = \frac{{\Delta \vec x}}{{\Delta t}}\)

- Tốc độ trung bình chỉ bằng độ lớn của vận tốc trung bình khi vật chuyển động thẳng không đổi chiều.

2. Vận tốc tức thời.

Xét trong một khoảng thời gian rất nhỏ, vận tốc trung bình sẽ trở thành vận tốc tức thời. Độ lớn của vận tốc tức thời chính là tốc độ tức thời.

3. Tổng hợp vận tốc.

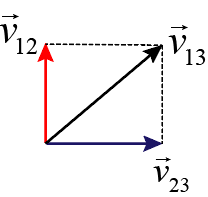
- Vector vận tốc tuyệt đối (vận tốc của vật đối với hệ quy chiếu đứng yên) bẳng tổng vector vận tốc tương đối (vận tốc của vật đối với hệ quy chiếu chuyển động) và vector vận tốc kéo theo (vận tốc của hệ quy chiếu chuyển động đối với hệ quy chiếu đứng yên)
- Gọi \(\vec v_{12}\) là vận tốc của vật 1 so với vật 2
\(\vec v_{23}\) là vận tốc của vật 2 so với vật 3
\(\vec v_{13}\) là vận tốc của vật 1 so với vật 3
Ta có:

\(\vec v_{13} = \vec v_{12} + \vec v_{23}\)

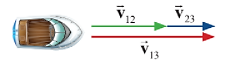
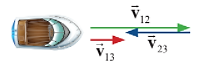
Khi \(\overrightarrow {{v_{12}}} \nearrow \nearrow \overrightarrow {{v_{23}}} \) thì: v₁₃= v₁₂ + v₂₃	Khi \(\overrightarrow {{v_{12}}} \nearrow \swarrow \overrightarrow {{v_{23}}} \) thì: v₁₃= v₁₂ - v₂₃	Khi \(\overrightarrow {{v_{12}}} \bot \overrightarrow {{v_{23}}} \) thì: \(v_{13}=\sqrt{v_{12}^2+v_{23}^2}\)

I. CÁCH ĐO TỐC ĐỘ TRONG PHÒNG THÍ NGHIỆM.

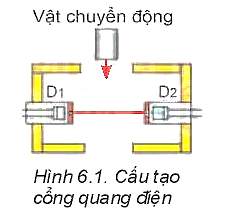
• Ta cần đo thời gian và quãng đường chuyển động của vật đó.

II. GIỚI THIỆU DỤNG CỤ ĐO THỜI GIAN.

1. Đồng hồ đo thời gian hiện số và cổng quang điện.

- Chức năng của một số nút trên đồng hồ:

+ MODE: Chọn kiểu làm việc cho máy đo thời gian.
+ MODE A: Đo thời gian vật chắn cổng quang điện nối với ổ A.
+ MODE B: Đo thời gian vật chắn cổng quang điện nối với ổ B.
+ MODE A + B: Đo tổng của hai khoảng thời gian vật chắn cổng quang điện nối với ôt A và vật chắn cổng quang điện nối với ổ B.
+ MODE A↔B: Đo thời gian vật chuyển động từ cổng quang điện nối với ổ A tới cổng quang điện nối với ổ B.
+ MODE T: Đo khoảng thời gian T của từng chu kì dao động.
+ Nút RESET: Đặt lại chỉ số của đồng hồ về giá trị 0.000.

- Cổng quang điện.

2. Thiết bị đo thời gian bằng cần rung.

- Dử dụng một cần rung đều đặn khoảng 50 lần trong 1 giây và đánh dấu các chấm trên băng giấy gắn vào xe chuyển động. Đo khoảng cách giữa các dấu chấm xác định được quãng đường đi được của xe trong 0,02s.

III. THỰC HÀNH ĐO TỐC ĐỘ CHUYỂN ĐỘNG.

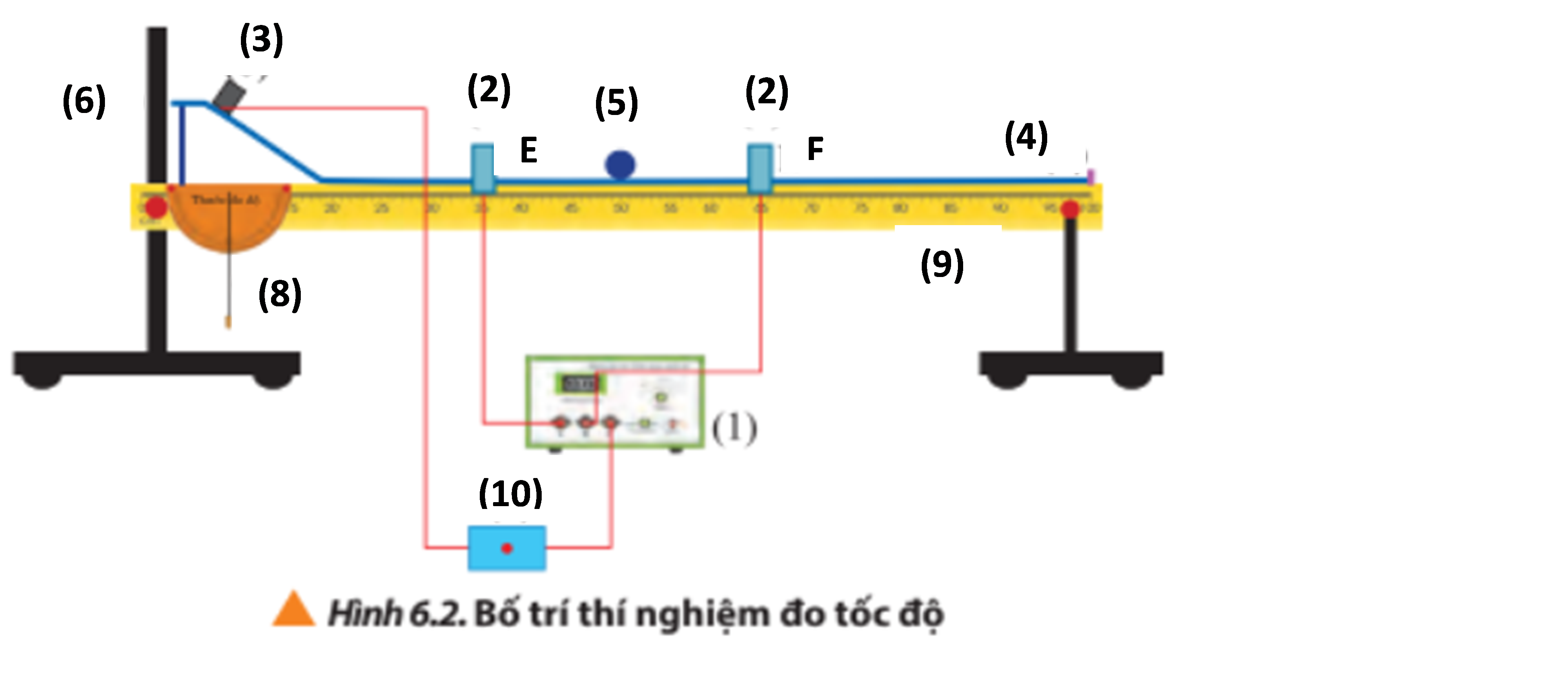
1. Dụng cụ thí nghiệm.

(1): đồng hồ đo thời gian hiện số MC964.
(2): cổng quang điện.
(3): nam châm điện và công tắc sử dụng để giữ/thả viên bi thép.
(4): máng có giá đỡ bằng hợp kim nhôm, có gắn thước đo góc và dây rọi.
(5): viên bi thép (6): giá đỡ có đế ba chân, có vít chỉnh cân bằng và trụ thép.
(7): thước cặp để đo đường kính viên bi thép.
(8): Thước đo độ có gắn dây dọi.
(9): Thước thẳng có độ chia nhỏ nhất 1mm.
(10): Công tắc điện.

2. Thiết kế phương án thí nghiệm.

Sử dụng bộ thí nghiệm đo tốc độ chuyển động của viên bi thép.

3. Tiến hành thí nghiệm.

- Thí nghiệm 1: Đo tốc độ trung bình

Bước 1	Bố trí thí nghiệm như hình 6.6
Bước 2	Nới vít hãm và đặt cổng quang điện E cách chân phần dốc của máng nghiêng.
Bước 3	Nôi hai cổng quang điện E, F với hai ổ cắm A, B ở mặt sau của đồng hồ đo thời gian.
Bước 4	Cắm nguồn điện của đồng hồ và bật công tắc nguồn đồng hồ đo thời gian hiện số, đặt MODE ở A↔B
Bước 5	Nới vít cổng quang điện, dịch chuyển đến vị trí thích hợp và vặn chặt để định vị. Đo quãng đường EF và ghi số liệu
Bước 6	Đặt viên bi thép lên máng nghiêng tại vị trí tiếp xúc với nam châm điện N và bị giữ lại ở đó
Bước 7	Nhấn nút RESET của đồng hồ đo thời gian hiện số để chuyển các số hiển thị về giá trị ban đầu 0.000
Bước 8	Nhấn nút của hộp công tắc kép để ngắt điện vào nam châm N: viên bi lăn xuống và chuyển động đi qua cổng quang điện E, F trên máng nghiêng
Bước 9	Ghi lại các giá trị thời gian hiển thị trên đồng hồ.
Bước 10	Thực hiện lại các thao tác 6, 7, 8, 9 ba lần và ghi các giá trị thời gian t tương ứng với quãng đường s
Chú ý: Khi cắm cổng quang điện vào ổ cắm A, B cần chú ý xoay đúng khe định vị, cắm thẳng giắc cắm, không rung, lắc chân cắm.

- Thí nghiệm 2: Đo tốc độ tức thời

Bước 1	Nới vít cổng quang điện, dịch chuyển đến vị trí thích hợp và vặn chặt để định vị
Bước 2	Sử dụng thước cặp đo đường kính viên bi
Bước 3	Bật công tắc nguồn đồng hồ đo thời gian hiện số, đặt MODE ở A hoặc B.
Bước 4	Đặt viên bi thép lên máng nghiêng tại vị trí tiếp xúc với nam châm điện N và bị giữ lại ở đó.
Bước 5	Nhấn nút RESET cả đồng hồ đo thời gian hiện số để chuyển các số hiển thị về giá trị ban đầu 0.000.
Bước 6	Nhấn nút của hộp công tắc kép để ngắt điện vào nam châm N: viên bi lăn xuống và chuyển động đi qua cổng điện trên máng nghiêng.
Bước 7	Ghi lại các giá trị thời gian hiển thị trên đồng hồ
Bước 8	Thực hiện lại các thao tác 4, 5, 6, 7 ba lần và ghi các giá trị t
Chú ý: Khi cắm cổng quang điện vào ổ cắm A, B cần chú ý xoay đúng khe định vị, cắm thẳng giắc cắm, không rung, lắc chân cắm.

4. Kết quả thí nghiệm.

- Quãng đường s = ......(m); Δs = ......(m).

Lần đo	Lần 1	Lần 2	Lần 3	Giá trịn tb	Sai số
Thời gian t (s)

- Đường kính viên bi d = ......(m); Δd = ......(m).

Lần đo	Lần 1	Lần 2	Lần 3	Giá trịn tb	Sai số
Thời gian t (s)

I. CHUYỂN ĐỘNG THẲNG.

- Chuyển động thẳng là chuyển động có quĩ đạo là đường thẳng.
- Khi chuyển động thẳng không đổi chiều, thì:
+ Quãng đường và độ dịch chuyển có độ lớn như nhau s = d.
+ Tốc độ và vận tốc có độ lớn như nhau v = ν.
- Khi vật chuyển động theo chiều âm của trục tọa độ thì:
+ Quãng đường có giá trị dương, còn độ dịch chuyển có giá trị âm.
+ Tốc độ có giá trị dương, còn vận tốc có giá trị âm.

II. ĐỒ THỊ ĐỘ DỊCH CHUYỂN - THỜI GIAN TRONG CHUYỂN ĐỘNG THẲNG.

Đồ thị độ dịch chuyển theo thời gian mô tả được chuyển động và cung cấp thêm nhiều thông tin khác.

1. Cách vẽ đồ thị độ dịch chuyển - thời gian (d-t) trong chuyển động thẳng đều.

- Trong chuyển động thẳng đều, đồ thị độ dịch chuyển theo thời gian có dạng là đường thẳng.

d = v.t

+ Nếu v > 0 thì đồ thị là đường thẳng hướng lên.
+ Nếu v < 0 thì đồ thị là đường thẳng hướng xuống.

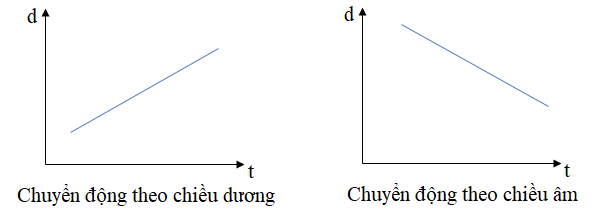- Cách vẽ đồ thì:
+ Lập bảng biến thiên.

Thời gian t (s)	t₁	t₂
Độ dịch chuyển d (m)	d₁	d₂

+ Xác định 2 điểm trên hệ tọa độ và nối 2 điểm đó lại.

2. Sử dụng đồ thị độ dịch chuyển - thời gian (d-t) trong chuyển động thẳng.

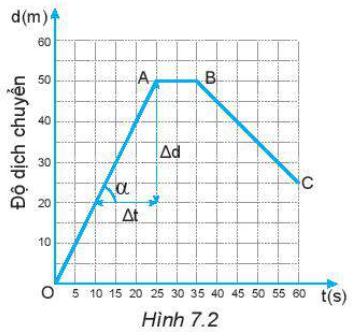Dựa vào đồ thị hình 7.2, hãy cho biết:
- Trong 25s đầu, mỗi giây người đó bơi được bao nhiêu mét? Tính vận tốc của người đó ra m/s.
- Từ giây nào tới giây nào, người đó không bơi?
- Từ giây thứ 35 đến giây thứ 60 người đó bơi theo chiều nào?
- Trong 20s cuối cùng, mỗi giây người đó bơi được bao nhiêu mét? Tính vận tốc của người đó ra m/s.
- Xác định độ dịch chuyển và vận tốc của người đó khi bơi từ B đến C?
- Xác định độ dịch chuyển và vận tốc của người đó trong cả quá trình bơi?

III. VẬN TỐC VÀ ĐỒ THỊ ĐỘ DỊCH CHUYỂN - THỜI GIAN TRONG CHUYỂN ĐỘNG THẲNG.

- Độ dốc của đồ thị độ dịch chuyển - thời gian trong chuyển động thẳng đều cho biết độ lớn của vận tốc chuyển động.
- Ví dụ, trong hình 7.2, trong giai đoạn OA thì vật có độ lớn vận tốc là:

\(v = \frac{\Delta d}{\Delta t}=\frac{50m}{25s}=2\frac{m}{s}\)

I. CHUYỂN ĐỘNG BIẾN ĐỔI.

- Chuyển động biến đổi là chuyển động có vận tốc biến đổi theo thời gian.

II. GIA TỐC CỦA CHUYỂN ĐỘNG BIẾN ĐỔI.

1. Khái niệm gia tốc.

- Gia tốc là 1 đại lượng vật lý đặc trưng cho sự biến thiên nhanh hay chậm của vận tốc.
- Gia tốc là đại lượng vector.

\({\vec a} = \frac{{\Delta {\bf{\vec v}}}}{{\Delta t}} = \frac{{\overrightarrow {{{\bf{v}}_2}} - {{{\bf{\vec v}}}_1}}}{{{t_2} - {t_1}}}\)

- Giá trị đại số của vectơ gia tốc tức thời gọi tắt là gia tốc và bằng:

\(a = \left|\frac{{\Delta {\bf{\vec v}}}}{{\Delta t}}\right|\)

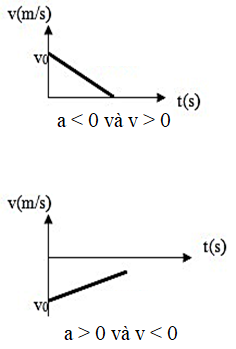
- Đơn vị của gia tốc a là m/s².
+ a.v > 0: chuyển động nhanh dần (\(\vec{a}\) cùng chiều \(\vec{v}\))
+ a.v < 0: chuyển động chậm dần (\(\vec{a}\) ngược chiều \(\vec{v}\))

2. Bài tập ví dụ.

Một xe máy đang chuyển động thẳng với vận tốc 10m/s thì tăng tốc. Biết rằng sau 5s kể từ khi tăng tốc, xe đạt vận tốc 12m/s.
a. Tính gia tốc của xe.
b. Nếu sau khi đạt vận tốc 12m/s, xe chuyển động chậm dần đều với gia tốc có độ lớn bằng gia tốc trên thì sau bao lâu xe sẽ dừng lại?

I. GIA TỐC CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU.

- Chuyển động thẳng biến đổi đều: là chuyển động có quỹ đạo là một đường thẳng và có vận tốc tức thời tăng đều hoặc giảm đều theo thời gian.

Chuyển động thẳng nhanh dần đều: là chuyển động có quỹ đạo là một đường thẳng và có vận tốc tức thời tăng đều theo thời gian.	Chuyển động thẳng chậm dần đều: là chuyển động có quỹ đạo là một đường thẳng và có vận tốc tức thời giảm đều theo thời gian.

- Gia tốc trong chuyển động thẳng biến đổi đều không đổi theo thời gian.

\(a = \frac{\vec v}{\Delta t}=hằng số.\)

II. VẬN TỐC TỨC THỜI CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU.

Nếu chọn gốc thời gian t₀ = 0, thì biểu thức vận tốc tức thời có dạng:

v = v₀ + a.t

III. ĐỒ THỊ VẬN TỐC - THỜI GIAN CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU.

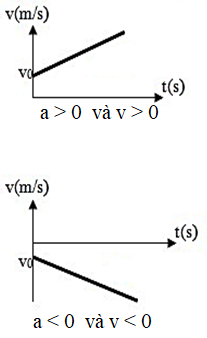
- Đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều có đường biểu diễn là 1 đường thẳng xiên góc, cắt trục tung tại điểm v = v₀.
- Từ định nghĩa gia tốc, ta có gia tốc tức thời tại một thời điểm có giá trị bằng độ dốc của đồ thị vận tốc – thời gian.
+ Đồ thị hướng lên: a > 0.
+ Đồ thị hướng xuống: a < 0
+ Đồ thị nằm ngang: a = 0
+ Hai đồ thị song song: Hai chuyển động có cùng gia tốc
+ Hai đồ thị cắt nhau: tại thời điểm đó hai vật chuyển động có cùng vận tốc (có thể cùng chiều hay khác chiều chuyển động)

Chuyển động thẳng nhanh dần đều.	Chuyển động thẳng chậm dần đều.

IV. ĐỘ DỊCH CHUYỂN CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU.

1. Tính độ dịch chuyển bằng đồ thị vận tốc - thời gian (v-t).

+ Độ dịch chuyển của vật trong khoảng thời gian từ t₁ đến t₂ được xác định bằng phần diện tích giới hạn bởi các đường v(t), v = 0 (trục hoành Ot), t = t₁, t = t₂ trong đồ thị (v - t).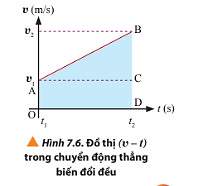

2. Tính độ dịch chuyển bằng công thức.

\(d = x = {{\rm{v}}_o}t + \frac{1}{2}a{t^2}\;\;\;\left( * \right)\)

\({{\rm{v}}^2} - {\rm{v}}_0^2 = 2ad\)

Từ (*) ta có đồ thị độ dịch chuyển theo thời gian có dạng parabol.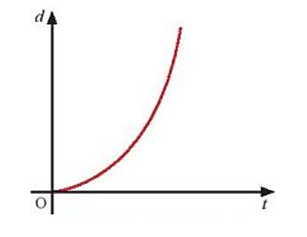

I. SỰ RƠI TRONG KHÔNG KHÍ.

- Sự rơi của các vật trong không khí là chuyển động thường gặp. VD: quả táo rơi từ trên cây xuống; chiếc lá rơi;...
- Sự rơi của các vật khác nhau trong không khí thì khác nhau.
- Nguyên nhân: do lực cản của không khí. Lực cản càng nhỏ so với trọng lực tác dụng lên vật thì vật sẽ rơi càng nhanh và ngược lại.

II. SỰ RƠI TỰ DO.

1. Sự rơi tự do.

- Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực - Nếu vật rơi trong không khí mà độ lớn của lực cản không khí không đáng kể so với trọng lượng của vật thì cũng coi là rơi tự do.

2. Đặc điểm của chuyển động rơi tự do.

a. Phương và chiều của chuyển động rơi tự do: Phương thẳng đứng, chiều từ trên xuống dưới.
b. Tính chất của chuyển động rơi tự do: là chuyển động thẳng nhanh dần đều.
c. Gia tốc rơi tự do:
- Ở cùng một nơi trên Trái Đất, mọi vật rơi tự do với cùng một gia tốc.
- Kí hiệu gia tốc rơi tự do là: g
+ g phụ thuộc vào vĩ độ địa lí và độ cao.
+ Ở gần bề mặt Trái Đất, g = 9,8 m/s².

3. Công thức rơi tự do.

- Rơi tự do có các công thức của chuyển động nhanh dần đều không vận tốc ban đầu: v₀ = 0
- Chọn thời điểm ban đầu t₀ = 0. Ta có:
+ Độ dịch chuyển và quãng đường đi được tại thời điểm t:

\(d=s=\frac{1}{2}gt^2\)

+ Vận tốc tức thời tại thời điểm t:

\(v=gt\)

+ Mối liên hệ giữa vận tốc, gia tốc và quãng đường đi được:

\(v^2=2gs\)

I. DỤNG CỤ THÍ NGHIỆM.

Bộ dụng cụ thí nghiệm đo gia tốc rơi tự do:
- Máng đứng có gắn dây dọi (1)
- Vật bằng thép hình trụ (2)
- Nam châm điện N, dùng giữ và thả trụ thép (3)
- Cổng quang điện E (4)
- Giá đỡ có đế ba chân, có vít chỉnh cân bằng và trụ thép (5)
- Đồng hồ đo thời gian hiện số (6)
- Công tắc kép (7)

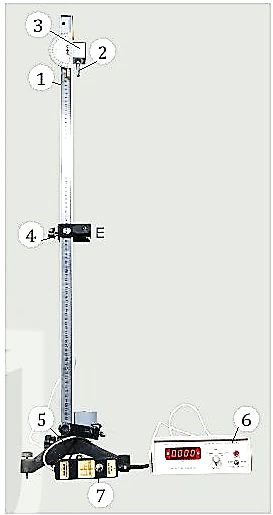
II. THIẾT KẾ PHƯƠNG ÁN THÍ NGHIỆM.

- Đo gián tiếp gia tốc rơi tự do thông qua đo thời gian và quãng đường chuyển động của vật theo công thức:

\(g=\frac{2s}{t^2}\)

- Thiết kế phương án thí nghiệm như bộ dụng cụ thí nghiệm đo gia tốc rơi tự do.

III. TIẾN HÀNH THÍ NGHIỆM.

- Bước 1. Bố trí thí nghiệm như hình.
- Bước 2. Cắm nam châm điện vào ổ A và cổng quang điện vào ổ B ở mặt sau của đồng hồ đo thời gian hiện số.
- Bước 3. Đặt MODE đồng hồ đo thời gian hiện số ở chế độ thích hợp A ↔ B
- Bước 4. Đặt trụ thép tại vị trí tiếp xúc với nam châm điện N và bị giữ lại ở đó
- Bước 5. Nhấn nút RESET của đồng hồ MC964 để chuyển các số hiển thị về giá trị ban đầu 0.000.
- Bước 6. Nhấn nút của hộp công tắc kép để ngắt điện vào nam châm điện. Trụ thép rơi xuống và chuyển động đi qua cổng quang điện
- Bước 7. Ghi lại các giá trị thời gian hiển thị trên đồng hồ
- Bước 8. Dịch chuyển cổng quang điện ra xa dần nam châm điện, thực hiện lại các thao tác 3, 4, 5, 6 bốn lần nữa. Ghi lại thời gian t tương ứng với quãng đường s.

IV. KẾT QUẢ THÍ NGHIỆM.

Quãng đường	Lần đo thời gian
Quãng đường	Lần 1	Lần 2	Lần 3	Lần 4	Lần 5
s₁
s₂
s₃
s₄
s₅

- Tính giá trị trung bình:

\(\overline{g}=.......\)

- Sai số tuyệt đối:

\(\Delta{g}\)

- Trình bày kết quả đo:

\(g =\overline{g} \pm \Delta{g}\)

I. CHUYỂN ĐỘNG NÉM NGANG.

1. Khái niêm chuyển động ném ngang.

- Chuyển động ném ngang là chuyển động có vận tốc ban đầu theo phương nằm ngang và chuyển động dưới tác dụng của trọng lực.

2. Thí nghiệm.

Dùng búa đập nhẹ thanh thép giữ bi B, thanh thép chuyển động thả bi B rơi tự do, đồng thời đẩy bi A theo phương nằm ngang khỏi giá đở với vận tốc v₀.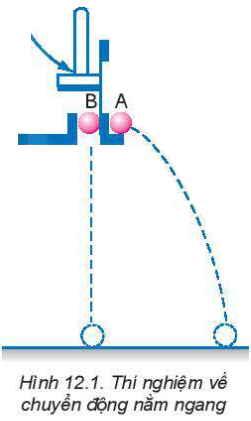

3. Phân tích kết quả thí nghiệm.

- Chuyển động ném ngang có quỹ đạo là một nhánh parabol. Hình chiếu chuyển động theo phương nằm ngang (Ox) là chuyển động thẳng đều, lên phương thẳng đứng (Oy) là rơi tự do.

- Chọn hệ trục tọa độ Oxy:
+ Gốc O là vị trí ném vật.
+ Trục 0x theo hướng vận tốc đầu.
+ Trục 0y thẳng đứng hướng xuống.
+ Gốc thời gian lúc ném.

- Theo phương Ox: M_x chuyển động thẳng đều với vận tốc v₀:

\(v_x=v_0\)

\(a_x=0\)

\(d_x=v_0.t\)

- Theo phương Oy: M_y chuyển động rơi tự do:

\(v_y=gt\)

\(a_y=g\)

\(d_y=\frac{1}{2}gt^2\)

- Thời gian vật chuyển động:

\(t=\sqrt{\frac{2H}{g}}\)

- Tầm bay xa:

\(L=d_{max}=v_0.t=v_0\sqrt{\frac{2H}{g}}\)

- Vận tốc ở thời điểm t:

\(v=\sqrt{v_x^2+v_y^2}=\sqrt{v_x^2+(gt)^2}\)

II. CHUYỂN ĐỘNG NÉM XIÊN.

Phân tích chuyển động ném xiên và công thức xác định tầm cao và tầm xa của chuyển động ném xiên.

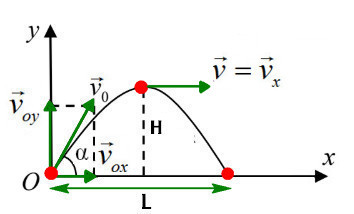- Chuyển động ném ngang có quỹ đạo là một parabol.
+ Hình chiếu chuyển động theo phương nằm ngang (Ox) là chuyển động thẳng đều
+ Hình chiếu chuyển động lên phương thẳng đứng (Oy) đi lên nhanh dần đều, đi xuống chậm dần đều.

- Chọn hệ trục tọa độ Oxy:
+ Gốc O là vị trí ném vật.
+ Trục 0x theo hướng vận tốc đầu.
+ Trục 0y thẳng đứng hướng lên.
+ Gốc thời gian lúc ném.

- Theo phương Ox: M_x chuyển động thẳng đều với vận tốc v_x:

\(v_x=v_0.cos(\alpha)\)

\(a_x=0\)

\(d_x=v_0.cos(\alpha).t\)

- Theo phương Oy: M_y chuyển động thẳng đi lên nhanh dần đều, đi xuống chậm dần đều:

\(v_y=v_0.sin(\alpha)-gt\)

\(a_y=-g\)

\(d_y=v_0.sin(\alpha)t-\frac{1}{2}gt^2\)

- Thời gian vật chuyển động:

\(t=\frac{2v_0.sin(\alpha)}{g}\)

- Tầm bay xa:

\(L=d_{max}=\frac{v_0^2.sin(2\alpha)}{g}\)

- Vận tốc ở thời điểm t:

\(v=\sqrt{v_x^2+v_y^2}=\sqrt{v_x^2+(gt)^2}\)

- Tầm bay cao:

\(H=\frac{v_0^2.sin^2(\alpha)}{2g}\)

- Phương trình quĩ đạo:

\(H=\frac{v_0^2.sin^2(\alpha)}{2g}\)

⇒ Quỹ đạo chuyển động của vật ném xiên là một parabol.

* Một số kí hiệu cần nhớ:

Vật lí Phổ thông

Chuyên trang Trắc nghiệm Trực tuyến

Thiết kế: Ths. Nguyễn Đăng Hân - 09133.90441

Động học