Vật lý

I. CHUYỂN ĐỘNG VÀ TƯƠNG TÁC CỦA CÁC PHÂN TỬ KHÍ.

1. Chuyển động Brown trong chất khí.

- Chuyển động Brown không chỉ xảy ra trong chất lỏng mà xảy ra cả trong chất khí.

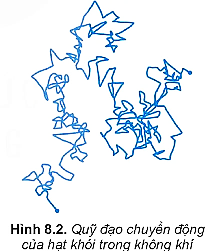
- Bằng thực nghiệm ta có kết luận sau:

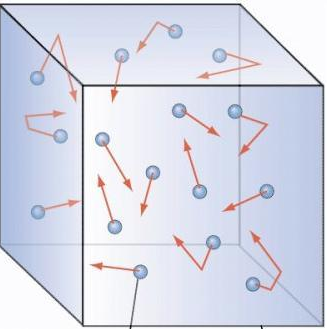
+ Chất khí được cấu tạo từ các phân tử chuyển động hỗn loạn, không ngừng.

+ Nhiệt độ của khí càng cao thì tốc độ chuyển động hỗn loạn của các phân tử khí càng lớn.

- Do các phân tử chuyển động hỗn loạn không ngừng, vận tốc luôn thay đổi do chúng va chạm với nhau và va chạm với thành bình. Do đó, ở đây chúng ta sẽ sử dụng tốc độ trung bình phân tử. Tốc độ này có tính thống kê và được xác định bởi:

\(\overline v = \frac{{{v_1} + {v_2} + ... + {v_N}}}{N}\)

Ví dụ, ở điều kiện tiêu chuẩn (T = 273K và p = 1atm), các phân tử khí chuyển động với tốc độ trung bình khoảng 400m/s.

2. Tương tác giữa các phân tử khí.

Giữa các phân tử khí cũng có lực đẩy và lực hút, gọi chung là lực liên kết. Vì khoảng cách giữa các phân tử khí rất lớn nên lực liên kết giữa các phân tử khí rât yếu so với thể lỏng và thể rắn.

II. MÔ HÌNH ĐỘNG HỌC PHÂN TỬ CHẤT KHÍ.

Nội dung mô hình động học phân tử chất khí:

- Chất khí được cấu tạo từ các phân tử có kích thước rất nhỏ so với khoảng cách giữa chúng.

- Các phân tử khí chuyển động hỗn loạn không ngừng; chuyển động này càng nhanh thì nhiệt độ chất khí càng cao.

- Khi chuyển động hỗn loạn các phân tử khí va chạm vào thành bình tác dụng lực, gây áp suất lên thành bình.

III. KHÍ LÍ TƯỞNG.

Ta có thể coi một chất khí ở điều kiện nhiệt độ và áp suất khí quyển bình thường gần đúng là một khí lí tưởng. Mô hình khí lí tưởng gồm các nội dung sau:

- Các phân tử khí được xem như chất điểm, có thể bo qua kích thước và thể tich của phân tử.

- Các phân tử khí không tương tác với nhau khi chưa va chạm.

- Các phân tử khí tương tác khi va với nhau và va chạm với thành bình. Các va chạm này là hoàn toàn đàn hồi.

I. CÁC THÔNG SỐ TRẠNG THÁI CỦA MỘT LƯỢNG KHÍ.

- Trạng thái của một lượng khí được xác định bằng 3 thông số trang thái: Áp suất (p); Thể tích (V); Nhiệt độ (T)

trong đó T là nhiệt độ tuyệt đối (K): T(K) = t(⁰C) + 273

- Thông thường, khi một lượng khí chuyển từ trạng thái này sang trạng thái khác thì cả 3 thông số sẽ biến đổi biến đổi. Tuy nhiên, có những quá trình biến đổi trạng thái mà còn một thông số không đổi thì các quá trình này gọi là đẳng quá trình.

II. ĐỊNH LUẬT BOYLE

1. Quá trình đẳng nhiệt.

Quá trình đẳng nhiệt: là quá trình biến đổi trạng thái của một khối lượng khí xác định trong đó nhiệt độ được giữ không đổi.

\(T_1=T_2\)

2. Thí nghiệm.

a. Chuẩn bị:

- Xilanh trong suốt có độ chia nhỏ nhất 0,5cm³ (1).

- Pittong có ống nối khí trong xilanh với áp kế (2).

- Áp kế có độ chia nhỏ nhất 0,05.10⁵Pa (3).

- Giá đỡ thí nghiệm (4).

- Thước đo (5).

b. Tiến hành.

- Bố trí thí nghiệm như hình.

- Dịch chuyển từ từ pittong để làm thay đổi thể tích khí.

- Đọc và ghi số liệu vào bảng 9.1.

Bảng 9.1.

Lần thí nghiệm	Thể tích V (cm³)	Áp suất P (10⁵Pa)
1	3,0
2	2,5
3	2,0
4	1,5

3. Định luật Boyle.

- Khi nhiệt độ của một khối lượng khí xác định giữ không đổi thì áp suất gây ra bởi khí tỉ lệ nghịch với thể tích của nó

\(p_1V_1=p_2V_2 = hằng số\)

hay

\(p \sim \frac{1}{V}\)

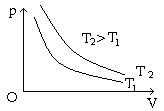
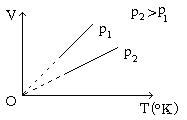
* Đường đẳng nhiệt: Là đường biểu diễn sự biến thiên của áp suất theo thể tích khi nhiệt độ không đổi. Trong hệ toạ độ OpV đường đẳng nhiệt là đường hypebol; trong hệ OTp hay OTV đường đẳng nhiệt là đường vuông góc với trục OT.

I. ĐỊNH LUẬT CHARLES.

1. Quá trình đẳng áp.

Quá trình đẳng áp: là quá trình biến đổi trạng thái của một khối lượng khí xác định trong đó áp suất được giữ không đổi.

\(p_1=p_2\)

2. Nghiên cứu của Charles.

- Bằng thực nghiệm, khi áp suất không đổi, Charles phát hiện:

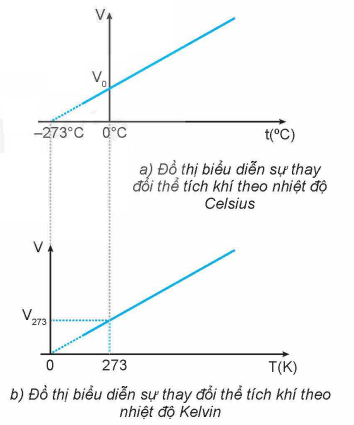
\(V=V_0(1+\alpha t)\)

trong đó: V₀ là thể tích khí ở nhiệt độ 0⁰C.

V là thể tích khí ở nhiệt độ t⁰C.

\(\alpha = \frac{1}{273}\)

3. Định luật Charles.

- Khi áp suất của một khối lượng khí xác định giữ không đổi thì thể tích của khí tỉ lệ thuận với nhiệt độ tuyệt đối của nó.

\(\frac{V_1}{T_1}=\frac{V_2}{T_2}= hằng số\)

hay

\(V \sim T\)

* Đường đẳng áp: Đường biểu diễn sự biến thiên của thể tích theo nhiệt độ khi áp suất không đổi gọi là đường đẵng áp. Trong hệ toạ độ OVT đường đẳng tích là đường thẳng kéo dài qua gốc toạ độ; trong hệ OpT hay OpV đường đẳng áp là đường vuông góc với trục Op.

II. THÍ NGHIỆM MINH HỌA ĐỊNH LUẬT CHARLES.

a. Chuẩn bị:

- Xilanh thủy tinh dung tích 50ml, có độ chia nhỏ nhất 1ml. (1)

- Nhiệt kế điện tử. (2)

- Ba cốc thủy tinh. (3) (4) (5)

- Nút cao sư để bịt đầu ra của xilanh.

- Giá đỡ thí nghiệm (6).

- Nước đá, nước nóng, nước ấm.

- Dầu bôi trơn.

b. Tiến hành.

- Bố trí thí nghiệm như hình.

- Cho một ít dầu bôi trơn để pittong dễ dàng duy chuyển trong xilanh. Điều chỉnh pittong ở mức 30ml, bịt đầu ra của xilanh bằng nút cao su.

- Ghi giá trị nhiệt độ phòng và thể tích khí trong xilanh.

- Đổ nước đá vào cốc (3).

- Nhúng xilanh và nhiệt kế vào cốc. Sau khoảng 3 phút, ghi giá trị thể tích khí trong xilanh và nhiệt độ t.

- Tiến hành thí nghiệm tương tự với cốc nước ấm (4) và cốc nước nóng (5).

- Đọc và ghi số liệu vào bảng 10.1.

Bảng 10.1.

Lần thí nghiệm	t(⁰C)	T (K)	Thể tích V (ml)
1
2
3
4

III. BÀI TẬP.

Bài 1: Khi tăng nhiệt độ của một lượng khí xác định từ 32⁰C lên 117⁰C và giữ áp suất không đổi thì thể tích tăng thêm 1,7 lít. Tìm thể tích của lượng khí trước và sau khi tăng nhiệt độ.

Bài 2: Thể tích của một lượng khí xác định tăng thêm 10% khi nhiệt độ của khí được tăng tới 47⁰C. Xác định nhiệt độ ban đầu của lượng khí, biết quá trình trên là quá trình đẳng áp.

Bài 3: Một khối lượng khí 12g có thể tích 4 lít ở nhiệt độ 7⁰C. Sau khi được đun nóng đẳng áp thì khối lượng riêng của khí là 1,2g/lít. Xác định nhiệt độ của khí sau khi đun nóng.

IV. CÁC ĐỊNH LUẬT BOYLE VÀ CHARLES LÀ CÁC ĐỊNH LUẬT GẦN ĐÚNG.

- Các kết quả thí nghiệm của Boyle và Charles đúng trong điều kiện áp suất không quá 10⁶Pa và nhiệt độ không dưới 200K. Nếu áp suất rất cao hay nhiệt độ rất thấp thì định luật trên không còn đúng.

- Khí lí tưởng tuân theo đúng định luật Boyle và Charles.

- Khí thực ở điều kiện bình thường (áp suất không quá lớn, nhiệt độ không quá thấp) có thể coi gần đúng tuân theo định luật Boyle và Charles.

I. PHƯƠNG TRÌNH TRẠNG THÁI CỦA KHÍ LÍ TƯỞNG.

1. Phương trình trạng thái của một lượng khí xác định.

Xét một khối khí biến đổi theo quá trình sau:

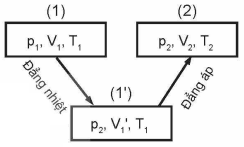
- Trạng thái 1 (p₁, V₁, T₁) biến đổi đẳng nhiệt sang trạng thái 2 (p₂, V'₁, T₁).

Ta có: \(p_1.V_1=p_2.V'_1\)

suy ra \(V'_1=\frac{p_1.V_1}{p_2}\)

- Trạng thái 2 (p₂, V'₁, T₁) biến đổi đẳng áp sang trạng thái 2 (p₂, V₂, T₂).

Ta có: \(\frac{V'_1}{T_1}=\frac{V_2}{T_2}\)

Thay biểu thức của \(V'_1\) và ta được:

Suy ra:

\(\frac{p_1.V_1}{T_1}=\frac{p_2.V_2}{T_2}\)

Đây được gọi là phương trình trạng thái khí lí tưởng.

2. Phương trình Clapeyron.

\(n=\frac{p.V}{RT}\)

trong đó n là số mol; V là thể tích (m³); p là áp suất (Pa); R=8,31 \(\frac{J}{mol.K}\); T là nhiệt độ tuyệt đối (K); M là khối lượng mol (g/mol); m là khối lượng (g); N_A là hằng số Avogadro

\(n=\frac{m}{M}=\frac{N}{N_A}=\frac{V_{đktc}}{22,4}\)

II. VẬN DỤNG.

Phương trình trạng thái của khí lý tưởng có nhiều ứng dụng thực tế.

- Nghiên cứu, chế tạo các thiết bị có liên quan đến chất khí như khí cầu, bình đựng khí, trang phục lặn, máy điều hòa không khí, máy nén khí,…

- Nghiên cứu sự thay đổi áp suất và thể tích của các lớp khí tồn tại trong các vật liệu để tìm tòi, sản xuất các vật liệu đáp ứng các yêu cầu sử dụng khác nhau; ứng dụng trong nghiên cứu về khí quyển, dự báo thời tiết,…

I. ÁP SUẤT KHÍ THEO MÔ HÌNH ĐỘNG HỌC PHÂN TỬ.

1. Tác dụng của một phân tử khí lên thành bình.

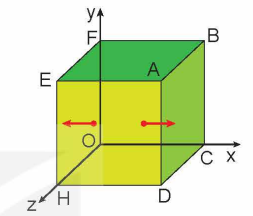
- Xét một lượng khí gồm N phân tử chứa trong một bình lập phương có cạnh l, trong hệ tọa độ vuông góc Oxyz.

- Một phân tử khối lượng m chuyển động thẳng đều song song với trục Ox với tốc độ v tới va chạm đàn hồi. Sau va chạm, phân tử chuyển động theo chiều ngược lại với tốc độ có cùng độ lớn v tới thành bình đối diện.

- Độ biến thiên động lượng của phân tử do va chạm có độ lớn là:

\(\left| {{\rm{\Delta \vec p}}} \right| = \left| { - {\rm{mv}} - \left( { + {\rm{mv}}} \right)} \right| = \left| { - 2{\rm{mv}}} \right| = 2{\rm{mv}}\)

- Áp suất của một phân tử khí tác dụng lên thành bình là:

\(p_m=\frac{m}{V}{v^2}\)

với v: tốc độ chuyển động của phân tử.

V: thể tích lượng khí.

\(\vec{p}\) là vector động lượng.

p là áp suất của chất khí.

p_m là áp suất của 1 phân tử khí.

2. Tác dụng của N phân tử khí lên thành bình.

Trung bình mỗi phân tử tác dụng lên thành bình một áp suất:

\(\overline {p_m} = \frac{m}{V} \cdot \overline {{v^2}} \)

trong đó: \(\overline {{v^2}} \;\)là trung bình của các bình phương tốc độ:

\(\overline {{v^2}} = \frac{{v_1^2 + v_2^2 + \ldots + v_N^2}}{N}\)

Áp suất khí tác dụng lên thành bình:

\(p = \frac{N}{3}p_m = \frac{N}{3}\frac{m}{V}\overline {{v^2}}= \frac{1}{3}\rho\overline {{v^2}} = \frac{1}{3}\mu {m}\overline {{v^2}} = \frac{2}{3}\mu \overline {{E_{{đ }}}} \)

trong đó:

\(\rho\): khối lượng riêng của khí (kg/m³).

\(\mu = \frac{N}{V}\): mật độ phân tử.

\(\overline{E_{đ}}=\frac{1}{2}m\overline{v^2}\): động năng trung bình của phân tử.

II. MỐI QUAN HỆ GIỮA ĐỘNG NĂNG PHÂN TỬ VÀ NHIỆT ĐỘ.

Từ \(p=\frac{nRT}{V}\) và \(p=\frac{2}{3}\frac{N}{V}\overline{E_đ}\), ta suy ra được:

– Liên hệ giữa động năng trung bình của 1 phân tử khí và nhiệt độ:

\(\overline {{E_{đ}}} = \frac{3}{2}kT\)

với k là hằng số Boltzmann

\(k = \frac{R}{N_A} = 1,38.10^{-23}\frac{J}{K}\)

– Liên hệ giữa áp suất và nhiệt độ:

\(p = \mu kT\)

1 Joules = 0.238846 Calo; 1Calo = 4184 J
1atm=101325Pa = 760mmHg =1,033 at;
Pa là paxcan (1 Pa = 1 N/m²)
1mmHg = 1/760 atm = 133,32 Pa

Câu 1. Thuyết động học phân tử chất khí.

- Chất khí được cấu tạo từ các phân tử có kích thước rất nhỏ so với khoảng cách giữa chúng.

- Các phân tử khí chuyển động hỗn loạn không ngừng; chuyển động càng nhanh thì nhiệt độ của chất khí càng cao.

- Khi chuyển động hỗn loạn các phân tử khí va chạm vào nhau và va chạm vào thành bình gây áp suất lên bình.

Câu 2. Khí lí tưởng: Là chất khí trong đó các phân tử được coi là các chất điểm và chỉ tương tác khi va chạm (thế năng của các phân tử khí lí tưởng bằng 0).

Câu 3. Phương trình trạng thái khí lí tưởng.

\(n=\frac{m}{M}=\frac{N}{N_A}=\frac{pV}{RT}\)

trong đó n là số mol; V là thể tích (m³); p là áp suất (Pa); R=8,31 \(\frac{J}{mol.K}\); T là nhiệt độ tuyệt đối (K); M là khối lượng mol (g/mol); m là khối lượng (g); N_A là hằng số Avogadro

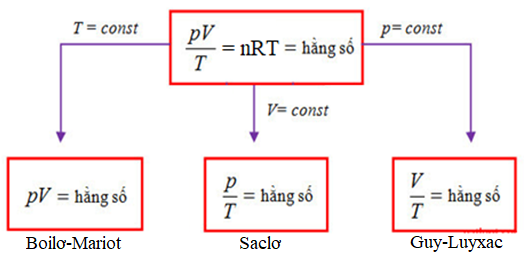
Câu 4. Quá trình đẳng nhiệt (T₁=T₂). Là quá trình biến đổi trạng thái trong đó nhiệt độ được giữ không đổi.

* Định luật Boyle - Mariotte: Trong quá trình đẵng nhiệt của một khối lượng khí xác định, áp suất tỉ lệ nghịch với thể tích.

\(p_1V_1=p_2V_2 = hằng số\)

hay

\(p \sim \frac{1}{V}\)

* Đường đẳng nhiệt: Là đường biểu diễn sự biến thiên của áp suất theo thể tích khi nhiệt độ không đổi. Trong hệ toạ độ OpV đường đẳng nhiệt là đường hypebol; trong hệ OTp hay OTV đường đẳng nhiệt là đường vuông góc với trục OT.

Câu 5. Quá trình đẳng tích (V₁=V₂). Là quá trình biến đổi trạng thái trong đó thể tích được giữ không đổi.

* Định luật Gay - Lussac: Trong quá trình đẵng tích của một khối lượng khí xác định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.

\(\frac{p_1}{T_1}=\frac{p_2}{T_2}= hằng số\)

hay

\(p \sim T\)

* Đường đẳng tích: Đường biểu diễn sự biến thiên của áp suất của một lượng khí theo nhiệt độ khi thể tích không đổi gọi là đường đẵng tích. Trong hệ toạ độ OpT đường đẳng tích là đường thẳng kéo dài đi qua gốc toạ độ.; trong hệ OVT hay OVp đường đẳng tích là đường vuông góc với trục OV.

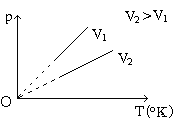
Câu 6. Quá trình đẳng áp (p₁=p₂). Là quá trình biến đổi trạng thái trong đó áp suất được giữ không đổi.

* Định luật Charles: Trong quá trình đẵng áp của một khối lượng khí xác định, thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.

\(\frac{V_1}{T_1}=\frac{V_2}{T_2}= hằng số\)

hay

\(V \sim T\)

* Đường đẳng áp: Đường biểu diễn sự biến thiên của thể tích theo nhiệt độ khi áp suất không đổi gọi là đường đẵng áp. Trong hệ toạ độ OVT đường đẳng tích là đường thẳng kéo dài qua gốc toạ độ; trong hệ OpT hay OpV đường đẳng áp là đường vuông góc với trục Op.

Câu 7. Động năng trung bình của 1 phân tử khí.

\(\overline {{E_{\rm{đ}}}} = \frac{1}{2}{m_m}\overline {{v^2}} \)

trong đó m_m là khối lượng 1 phân tử khí, và

\(\overline {{v^2}} = \frac{{v_1^2 + v_2^2 + v_3^2 + ....v_N^2}}{N}\)

là trung bình của bình phương vận tốc các phân tử khí.

- Liên hệ giữa động năng trung bình của 1 phân tử khí và áp suất:

\(p = \frac{1}{3}\mu {m_m}\overline {{v^2}} = \frac{2}{3}\mu \overline {{E_{{đ }}}} \)

trong đó

\(\mu = \frac{N}{V}\)

là mật độ phân tử và N là tổng số phân tử, V là thể tích, p là áp suất khí.

– Liên hệ giữa động năng trung bình của 1 phân tử khí và nhiệt độ:

\(\overline {{E_{đ}}} = \frac{3}{2}kT\)

với k là hằng số Boltzmann

\(k = \frac{R}{N_A} = 1,38.10^{-23}\frac{J}{K}\)

– Liên hệ giữa áp suất và nhiệt độ:

\(p = \mu kT\)

với k là hằng số Boltzmann

\(k = \frac{R}{N_A} = 1,38.10^{-23}\frac{J}{K}\)

- Một số công thức bổ sung:

+ Số phân tử khí trong bình:

\(N = \mu V = nN_A\)

+ Khối lượng một phân tử khí:

\({m_m} = \frac{m}{N} = \frac{M}{{{N_A}}} = \frac{\rho }{\mu }\)

với n là số mol khí, N_A là số Avôgađrô, ρ là khối lượng riêng của khí:

\(\rho = \frac{m}{V}\)

Vật lí Phổ thông

Chuyên trang Trắc nghiệm Trực tuyến

Thiết kế: Ths. Nguyễn Đăng Hân - 09133.90441

Khí lí tưởng