Vật lý

1. Chuyển động cơ: Chuyển động của một vật là sự thay đổi vị trí của vật đó so với các vật khác theo thời gian.

2. Chất điểm Những vật có kích thước rất nhỏ so với độ dài đường đi (hoặc với những khoảng cách mà ta đề cập đến), được coi là chất điểm.

- Khi một vật được coi là chất điểm thì khối lượng của vật coi như tập trung tại chất điểm đó.

3. Quỹ đạo: Quỹ đạo của chuyển động là đường mà chất điểm chuyển động vạch ra trong không gian.

4. Vật làm mốc và thước đo: Để xác định chính xác vị trí của vật ta chọn một vật làm mốc và một chiều dương trên quỹ đạo rồi dùng thước đo chiều dài đoạn đường từ vật làm mốc đến vật.

5. Hệ toạ độ:

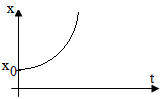
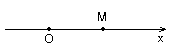
- Hệ toạ độ 1 trục (sử dụng khi vật chuyển động trên một đường thẳng). Toạ độ của vật ở vị trí M xác định bởi: x = $\overline {OM} $.

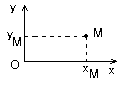
- Hệ toạ độ 2 trục (sử dụng khi vật chuyển động trên một đường cong trong một mặt phẳng). Toạ độ của vật ở vị trí M xác định bởi: (x_M, y_M)

6. Mốc thời gian và đồng hồ. Để xác định từng thời điểm ứng với từng vị trí của vật chuyển động ta phải chọn mốc thời gian và đo thời gian trôi đi kể từ mốc thời gian bằng một chiếc đồng hồ.

7. Thời điểm và thời gian. Vật chuyển động đến từng vị trí trên quỹ đạo vào những thời điểm nhất định còn vật đi từ vị trí này đến vị trí khác trong những khoảng thời gian nhất định.

8. Hệ qui chiếu. Một hệ qui chiếu gồm:

- Một vật làm mốc, một hệ toạ độ gắn với vật làm mốc.

- Một mốc thời gian và một đồng hồ.

9. Độ dời: là khoảng cách ngắn nhất giữa 2 điểm. Độ dời không phụ thuộc vào hình dạng của quỹ đạo chuyển động mà chỉ phụ thuộc vào vị trí điểm đầu và vị trí điểm cuối.

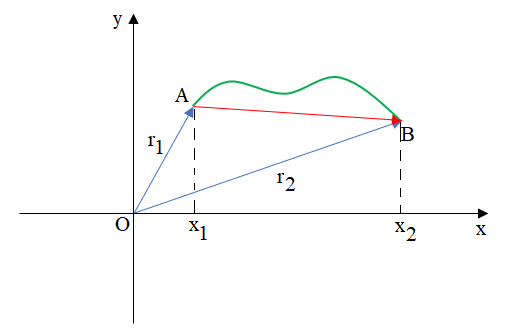
- Vectơ $\overrightarrow {AB} $ gọi là véctơ độ dời.

- Độ dời trên trục Ox là độ biến thiên tọa độ x.

$\Delta x = {x_{2}} - {x_{1}}$

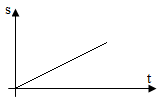
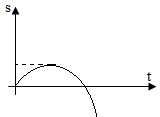
10. Quãng đường S: là độ dài quỹ đạo chuyển động của vật. Trong hình trên thì quãng đường chính là độ dài cung AB.

- Khi chất điểm chuyển động, quãng đường nó đi được có thể không trùng với độ dời của nó.

11. Vận tốc: Vận tốc là một đại lượng véctơ, đặc trưng cho sự chuyển động nhanh hay chậm của vật. Đơn vị là m/s.

- Vận tốc trung bình được tính bằng thương số của độ dời và thời gian tương ứng. Vận tốc trung bình có phương, chiều trùng với phương, chiều của véc tơ độ dời.

+ Với r₁, r₂ là tọa độ của chất điểm tại các thời điểm t₁ và t₁, thì ta có:

$\overrightarrow v_{tb} = \frac{{\overrightarrow r_2 - \overrightarrow {{r_1}} }}{{t_2 - t_1}} = \frac{{\Delta \overrightarrow r }}{{\Delta t}}$

+ Khi vật chuyển động trên trục Ox thì ta có:

${v_{tb}} = \frac{{\Delta x}}{{\Delta t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}$

- Tốc độ trung bình được tính bằng thương số của độ dài cung đi được và thời gian tương ứng.

${ v _{tb}} = \frac{S}{t}$

- Vận tốc tức thời tại một thời điểm t đặc trưng cho chiều và độ nhanh chậm của chuyển động tại thời điểm đó.

$\overrightarrow v = \frac{{\overrightarrow r_2 - \overrightarrow {{r_1}} }}{{t_2 - t_1}} = \frac{{\Delta \overrightarrow r }}{{\Delta t}}$ khi $\Delta t \to 0$.

+ Véctơ vận tốc của một vật gồm có:

. Điểm đặt: tại vật chuyển động.

. Phương: tiếp tuyến quỹ đạo.

. Chiều: cùng chiều chuyển động.

. Độ lớn: $v = \left| {\frac{{\Delta \overrightarrow r}}{{\Delta t}}} \right|$ khi $\Delta t$ rất bé.

+ Khi vật chuyển động trên trục Ox thì ta có:

${v} = \frac{{\Delta x}}{{\Delta t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}$ khi $\Delta t \to 0$.

- Tốc độ tức thời chính là độ lớn của vận tốc tức thời.

12. Gia tốc: Gia tốc là đại lượng vật lí đặc trưng cho khả năng thay đổi vận tốc của vật cả về hướng và độ lớn, nó được xác định bởi:

$\overrightarrow a = \frac{{\overrightarrow v - \overrightarrow {{v_0}} }}{{t - {t_0}}} = \frac{{\Delta \overrightarrow v }}{{\Delta t}}$ khi $\Delta t \to 0$

Trong đó:

$\overrightarrow v $ : vận tốc tức thời tại thời điểm t (thời điểm lúc sau)

$\overrightarrow {{v_0}} $: vận tốc tức thời tại thời điểm t₀ (thời điểm ban đầu)

$\Delta t = t - {t_0}$: thời gian vận tốc thay đổi từ $\overrightarrow {{v_0}} $ sang $\overrightarrow v $

Đơn vị của gia tốc: m/s².

- Véctơ gia tốc của một vật gồm có:

+ Điểm đặt: tại vật chuyển động.

+ Phương: cùng phương với vectơ $\overrightarrow{\Delta v} $.

+ Chiều: cùng chiều với $\overrightarrow{\Delta v} $.

+ Độ lớn: $a = \left| {\frac{\overrightarrow {\Delta v}}{{\Delta t}}} \right|$ khi $\Delta t \to 0$.

- Định nghĩa: Chuyển động thẳng là chuyển động có quĩ đạo đường thẳng.

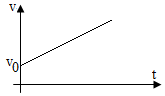
- Vận tốc tức thời: v = v₀ + at

- Quãng đường: s = v₀t + $\frac{1}{2}at^2$

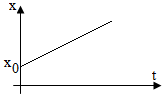
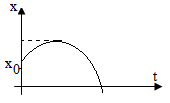
- Toạ độ: x = x₀ + v₀t + $\frac{1}{2}at^2$

- Công thức liên hệ : v₂ - v₀² = 2as

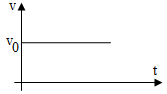
Chuyển động thẳng đều	- Định nghĩa: là chuyển động có quĩ đạo đường thẳng và vận tốc không đổi. - Đặc điểm: Gia tốc a = 0. - Vận tốc tức thời: v = v₀ - Quãng đường: s = v₀t - Toạ độ: x = x₀ + v₀t - Công thức liên hệ : v² - v₀² = 0
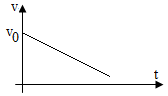
Chuyển động thẳng chậm dần đều	- Định nghĩa: là chuyển động có quĩ đạo đường thẳng và vận tốc giảm dần đều theo thời gian. - Đặc điểm: Gia tốc trái dấu với vận tốc v (a.v < 0). - Vận tốc tức thời: v = v₀ + at - Quãng đường: s = v₀t + $\frac{1}{2}at^2$ - Toạ độ: x = x₀ + v₀t + $\frac{1}{2}at^2$ - Công thức liên hệ : v² - v₀² = 2as
Chuyển động thẳng nhanh dần đều	- Định nghĩa: là chuyển động có quĩ đạo đường thẳng và vận tốc tăng dần đều theo thời gian. - Đặc điểm: Gia tốc cùng dấu với vận tốc v (a.v > 0). - Vận tốc tức thời: v = v₀ + at - Quãng đường: s = v₀t + $\frac{1}{2}at^2$ - Toạ độ: x = x₀ + v₀t + $\frac{1}{2}at^2$ - Công thức liên hệ : v² - v₀² = 2as
Rơi tự do	- Định nghĩa: Sự rơi tự do là sự rơi dưới tác dụng của trọng lực. - Đặc điểm: + Quĩ đạo: Đường thẳng. Phương thẳng đứng hướng từ trên xuống dưới. + Chuyển động thẳng nhanh dần đều. + Vận tốc ban đầu bằng không (v₀ = 0). + Gia tốc: g ≈ 10, hướng thẳng xuống. Càng lên cao g càng giảm. - Vận tốc tức thời: v = gt - Quãng đường: h = $\frac{1}{2}gt^2$ - Toạ độ: x = x₀ + $\frac{1}{2}gt^2$ - Công thức liên hệ : v² = 2gh

I. Định nghĩa.

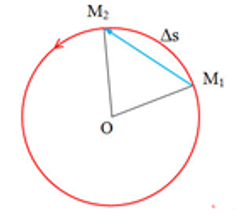
1. Chuyển động tròn: Chuyển động tròn là chuyển động có quỹ đạo là một đường tròn.

2. Tốc độ trung bình trong chuyển động tròn: Tốc độ trung bình của chuyển động tròn là đại lượng đo bằng thương số giữa độ dài cung tròn mà vật đi được và thời gian đi hết cung tròn đó.

$v_{tb} = \frac{s}{t}$

3. Chuyển động tròn đều: Chuyển động tròn đều là chuyển động có quỹ đạo tròn và có tốc độ trung bình trên mọi cung tròn là như nhau.

II. Vận tốc độ dài và vận tốc góc.

Vận tốc dài	Vận tốc góc

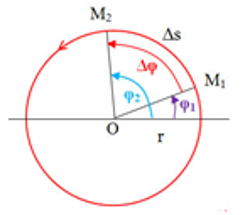
- Công thức: $\vec v = \frac{{\overrightarrow {\Delta s} }}{{\Delta t}}$ khi $\Delta t \to 0$ + Trong đó $\Delta s$ là độ dài cung quét được. + Trong đó $\Delta t$ là thời gian tương ứng. - Véctơ vận tốc dài gồm có: + Điểm đặt: tại vật chuyển động. + Phương: tiếp tuyến với đường tròn. + Chiều: cùng chiều với chuyển động. + Độ lớn: $v = \left\| {\frac{{\overrightarrow {\Delta s} }}{{\Delta t}}} \right\|$ khi $\Delta t \to 0$.	- Công thức: $\omega = \frac{\Delta \varphi}{\Delta t}$ + Trong đó $\Delta \varphi $ là góc quét được. + $\Delta t$ là thời gian tương ứng. + Đơn vị vận tốc góc là rad/s.
- Liên hệ giữa tốc độ dài và tốc độ góc: v = r.ω; với r là bán kính của quỹ đạo.

Tần số góc ω

Tần số f

Chu kì T

- Tần số góc chính bằng tốc độ góc.

- Đơn vị rad/s.

- Tần số là số vòng vật quay được trong 1 giây.

- Công thức: $f = \frac{\omega}{2\pi}$.

- Đơn vị: Hz.

- Chu kì là khoảng thời gian vật quay được 1 vòng.

- Công thức: $T = \frac{1}{f} = \frac{2\pi}{\omega}$.

- Đơn vị: s.

II. Gia tốc hướng tâm.

- Trong chuyển động tròn đều, mặc dù vận tốc có độ lớn không đổi, nhưng có hướng luôn thay đổi, nên chuyển động này có gia tốc.

- Vectơ gia tốc hướng tâm $\vec a_{ht}$ gồm có:

+ Điểm đặt: tại vật chuyển động.

+ Phương: trùng với đường thẳng nối từ vật vào tâm quĩ đạo.

+ Chiều: luôn hướng vào tâm quĩ đạo.

+ Độ lớn: $a_{ht} = \frac{v^2}{r} = r\omega^2$.

I. Tính tương đối của chuyển động.

1. Tính tương đối của quỹ đạo: Hình dạng quỹ đạo của chuyển động trong các hệ qui chiếu khác nhau thì khác nhau → quỹ đạo có tính tương đối

2. Tính tương đối của vận tốc: Vận tốc của vật chuyển động đối với các hệ qui chiếu khác nhau thì khác nhau → vận tốc có tính tương đối

II. Công thức cộng vận tốc.

1. Hệ qui chiếu đứng yên và hệ qui chiếu chuyển động.

- Hệ qui chiếu gắn với vật đứng yên gọi là hệ qui chiếu đứng yên.

- Hệ qui chiếu gắn với vật vật chuyển động gọi là hệ qui chiếu chuyển động.

2. Công thức cộng vận tốc.

- Nếu một vật (1) chuyển động với vận tốc ${\vec v_{12}}$ trong hệ qui chiếu số (2), hệ qui chiếu số (2) lại chuyển động với vận tốc ${\vec v_{23}}$ trong hệ qui chiếu số (3) thì trong hệ qui chiếu số (3) vật chuyển động với vận tốc ${\vec v_{13}}$ được tính theo công thức:

$\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} $

- Độ lớn của vận tốc:

Nếu $\overrightarrow {{v_{12}}} \uparrow \uparrow \overrightarrow {{v_{23}}} $ ${v_{13}} = v{}_{12} + {v_{23}}$
Nếu $\overrightarrow {{v_{12}}} \uparrow \downarrow \overrightarrow {{v_{23}}}$ $ {v_{13}} = \left\| {v{}_{12} - {v_{23}}} \right\|$
Nếu $\overrightarrow {{v_{12}}} \bot \overrightarrow {{v_{23}}}$ $ {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} $
Tổng quát: ${v_{13}} = \sqrt {v_{12}^2 + v_{23}^2 + 2{v_{12}}{v_{23}}{\rm{cos}}\alpha } $ Với $\alpha = \left( {\overrightarrow {{v_{12}}} ,\overrightarrow {{v_{23}}} } \right)$

I. Phép đo các đại lượng vật lí – hệ đơn vị SI.

1. Phép đo các đại lượng vật lí.

- Phép đo một đại lượng vật lí là phép so sánh nó với đại lượng cùng loại được qui ước làm đơn vị.

- Công cụ để so sánh gọi là dụng cụ đo.

- Đo trực tiếp : So sánh trực tiếp qua dụng cụ.

- Đo gián tiếp : Đo một số đại lượng trực tiếp rồi suy ra đại lượng cần đo thông qua công thức.

2. Đơn vị đo.

- Hệ đơn vị đo thông dụng hiện nay là hệ SI.

- Hệ SI qui định 7 đơn vị cơ bản: Độ dài: mét (m); thời gian: giây (s); khối lượng: kilôgam (kg); nhiệt độ : kenvin (K); cường độ dòng điện: ampe (A); cường độ sáng: canđêla (Cd); lượng chất: mol (mol).

II. Sai số của phép đo.

1. Sai số hệ thống: Là sự sai lệch do phần lẻ không đọc được chính xác trên dụng cụ (gọi là sai số dụng cụ $\Delta A'$ ) hoặc điểm 0 ban đầu bị lệch. Sai số dụng cụ $\Delta A'$ thường lấy bằng nửa hoặc một độ chia trên dụng cụ.

2. Sai số ngẫu nhiên: Là sự sai lệch do hạn chế về khả năng giác quan của con người do chịu tác động của các yếu tố ngẫu nhiên bên ngoài.

3. Giá trị trung bình.

$\overline A = \dfrac{{{A_1} + {A_2} + ... + {A_n}}}{n}$

4. Cách xác định sai số của phép đo.

- Sai số tuyệt đối của mỗi lần đo:

$\Delta {A_1} = \left| {\overline A - {A_1}} \right|; \Delta {A_2} = \left| {\overline A - {A_2}} \right|; \Delta {A_n} = \left| {\overline A - {A_n}} \right|$ ...

- Sai số tuyệt đối trung bình của n lần đo:

$\Delta \overline A = \dfrac{{\Delta {A_1} + \Delta {A_2} + ... + \Delta {A_n}}}{n}$

- Sai số tuyệt đối của phép đo là tổng sai số tuyệt đối trung bình và sai số dụng cụ:

$\Delta A = \Delta \overline A + \Delta A'$

5. Cách viết kết quả đo:

$A = \overline A \pm \Delta A$

6. Sai số tỉ đối.

$\delta A = \dfrac{{\Delta A}}{{\overline A }}.100\% $

7. Số chữ số có nghĩa trong kết quả đo: Số chữ số có nghĩa là những chữ số (kể cả chữ số 0) tính từ trái sang phải kể từ chữ số khác không đầu tiên.

Ví dụ:

+ $0,45\xrightarrow{{0,\left[ {45} \right]}}$ có 2 chữ số có nghĩa

+ $0,1079\xrightarrow{{0,\left[ {1079} \right]}}$ có 4 chữ số có nghĩa

+ $003,134\xrightarrow{{000\left[ {3,134} \right]}}$ có 4 chữ số có nghĩa

8. Cách xác định sai số của phép đo gián tiếp.

- Sai số tuyệt đối của một tổng hay hiệu thì bằng tổng các sai số tuyệt đối của các số hạng.

- Sai số tỉ đối của một tích hay thương thì bằng tổng các sai số tỉ đối của các thừa số.

- Nếu trong công thức vật lí xác định các đại lượng đo gián tiếp có chứa các hằng số thì hằng số phải lấy đến phần thập phân lẻ nhỏ hơn $\dfrac{1}{{10}}$ tổng các sai số có mặt trong cùng công thức tính.

- Nếu công thức xác định đại lượng đo gián tiếp tương đối phức tạp và các dụng cụ đo trực tiếp có độ chính xác tương đối cao thì có thể bỏ qua sai số dụng cụ.

Nếu \(\overrightarrow {{v_{12}}} \uparrow \uparrow \overrightarrow {{v_{23}}} \) \({v_{13}} = v{}_{12} + {v_{23}}\)
Nếu \(\overrightarrow {{v_{12}}} \uparrow \downarrow \overrightarrow {{v_{23}}}\) \( {v_{13}} = \left\| {v{}_{12} - {v_{23}}} \right\|\)
Nếu \(\overrightarrow {{v_{12}}} \bot \overrightarrow {{v_{23}}}\) \( {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} \)
Tổng quát: \({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2 + 2{v_{12}}{v_{23}}{\rm{cos}}\alpha } \) Với \(\alpha = \left( {\overrightarrow {{v_{12}}} ,\overrightarrow {{v_{23}}} } \right)\)

Vật lí Phổ thông

Chuyên trang Trắc nghiệm Trực tuyến

Thiết kế: Ths. Nguyễn Đăng Hân - 09133.90441

Cùng thầy Hân Luyện Vật lí 10

Cùng thầy Hân Luyện Vật lí 11

Cùng thầy Hân Luyện thi Tốt nghiệp

Vật lý Lớp 10

Chương 1: Động học chất điểm

Vận tốc dài	Vận tốc góc

- Công thức: \(\vec v = \frac{{\overrightarrow {\Delta s} }}{{\Delta t}}\) khi \(\Delta t \to 0\) + Trong đó \(\Delta s\) là độ dài cung quét được. + Trong đó \(\Delta t\) là thời gian tương ứng. - Véctơ vận tốc dài gồm có: + Điểm đặt: tại vật chuyển động. + Phương: tiếp tuyến với đường tròn. + Chiều: cùng chiều với chuyển động. + Độ lớn: \(v = \left\| {\frac{{\overrightarrow {\Delta s} }}{{\Delta t}}} \right\|\) khi \(\Delta t \to 0\).	- Công thức: \(\omega = \frac{\Delta \varphi}{\Delta t}\) + Trong đó \(\Delta \varphi \) là góc quét được. + \(\Delta t\) là thời gian tương ứng. + Đơn vị vận tốc góc là rad/s.
- Liên hệ giữa tốc độ dài và tốc độ góc: v = r.ω; với r là bán kính của quỹ đạo.