Vật lý Lớp 10

I. Lực. Cân bằng lực.

- Định nghĩa: Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.

- Đơn vị của lực là Niutơn (N).

- Các lực cân bằng là các lực khi tác dụng đồng thời vào một vật thì không gây ra gia tốc cho vật.

- Hai lực cân bằng là hai lực cùng tác dụng lên một vật, cùng giá, cùng độ lớn và ngược chiều.

- Hai lực trực đối là hai lực cùng giá, cùng độ lớn và ngược chiều, nhưng có điểm đặt khác nhau.

II. Tổng hợp lực.

1. Định nghĩa: Tổng hợp lực là thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt các lực ấy. Lực thay thế này gọi là hợp lực.

2. Qui tắc hình bình hành: Nếu hai lực đồng qui làm thành hai cạnh của một hình bình hành, thì đường chéo kể từ điểm đồng qui biểu diễn hợp lực của chúng.

\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)

Lưu ý: $ \left| {{F_1} - {F_2}} \right| ≤ F ≤ {F_1} + {F_2} $

Nếu \(\overrightarrow {{F_{1}}} \uparrow \uparrow \overrightarrow {{F_{2}}} \) \(F = F_1 + F_2\)
Nếu \(\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_{2}}}\) \( F = \left| {F_1 - F_2} \right|\)
Nếu \(\overrightarrow {{F_{1}}} \bot \overrightarrow {{F_{2}}}\) \( F = \sqrt {F_1^2 + F_2^2} \)
Tổng quát: \( F = \sqrt {F_1^2 + F_2^2 + 2{F_{1}}{F_{2}}{\rm{cos}}\alpha } \) Với \(\alpha = \left( {\overrightarrow {{F_{1}}} ,\overrightarrow {{F_{2}}} } \right)\)

III. Điều kiện cân bằng của chất điểm.

- Muốn cho một chất điểm đứng cân bằng thì hợp lực của các lực tác dụng lên nó phải bằng không.

\(\vec F_{hl} = \vec F_1 + \vec F_2 + \vec F_3 + ... = 0\)

IV. Phân tích lực

- Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó. Các lực thay thế gọi là các lực thành phần.

I. Định luật I Newton.

1. Định luật I Newton: Nếu một vật không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không. Thì vật đang đứng yên sẽ tiếp tục đứng yên, đang chuyển động sẽ tiếp tục chuyển động thẳng đều.

2. Quán tính: Quán tính là tính chất của mọi vật có xu hướng bảo toàn vận tốc của về hướng và độ lớn.

3. Hệ quy chiếu quán tính: Là hệ quy chiếu gắn vào vật mốc đứng yên hoặc chuyển động thẳng đều. Trong mọi hệ quy chiếu quán tính, các định luật vật lí diễn ra như nhau.

4. Hệ quy chiếu phi quán tính: Là hệ quy chiếu gắn vào vật mốc chuyển động có gia tốc. Trong hệ quy chiếu phi quán tính xuất hiện lực quán tính.

II. Định luật II Newton.

1. Định luật II Newton: Gia tốc của một vật cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật.

\(\overrightarrow a = \frac{{\overrightarrow F }}{m}\) hay \(\overrightarrow F = m\overrightarrow a \)

Trong trường hợp vật chịu nhiều lực tác dụng thì:

\(\overrightarrow a = \frac{{\overrightarrow F_{hl} }}{m} = \frac{{\overrightarrow F_1 + \overrightarrow F_2 + \overrightarrow F_3 + ... }}{m} \)

2. Khối lượng và mức quán tính.

- Định nghĩa: Khối lượng là đại lượng đặc trưng cho mức quán tính của vật.

- Tính chất của khối lượng.

  + Khối lượng là một đại lượng vô hướng, dương và không đổi đối với mỗi vật.

  + Khối lượng có tính chất cộng.

3. Trọng lực. Trọng lượng.

- Trọng lực là lực hút của Trái Đất tác dụng vào vật, gây ra cho chúng gia tốc rơi tự do. Trọng lực được kí hiệu là \(\vec P\). Trọng lực tác dụng lên vật gồm có.

  + Điểm đặt: tại trọng tâm của vật.

  + Phương: thẳng đứng.

  + Chiều: từ trên hướng xuống.

  + Độ lớn: P = mg.

- Trọng lượng: Độ lớn của trọng lực tác dụng lên một vật gọi là trọng lượng của vật, kí hiệu là P. Trọng lượng của vật được đo bằng lực kế.

III. Định luật III Newton.

1. Sự tương tác giữa các vật: Khi một vật tác dụng lên vật khác một lực thì vật đó cũng bị vật kia tác dụng ngược trở lại một lực. Ta nói giữa 2 vật có sự tương tác.

2. Định luật III Newton: Trong mọi trường hợp, khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng lại vật A một lực. Hai lực này có cùng giá, cùng độ lớn nhưng ngược chiều.

3. Lực và phản lực.

- Một trong hai lực tương tác giữa hai vật gọi là lực tác dụng còn lực kia gọi là phản lực.

- Đặc điểm của lực và phản lực:

  + Lực và phản lực luôn luôn xuất hiện (hoặc mất đi) một cách đồng thời.

  + Lực và phản lực có cùng giá, cùng độ lớn nhưng ngược chiều. Hai lực có đặc điểm như vậy gọi là hai lực trực đối.

  + Lực và phản lực không cân bằng nhau vì chúng đặt vào hai vật khác nhau.

I. Lực hấp dẫn. Mọi vật trong vũ trụ đều hút nhau với một lực, gọi là lực hấp dẫn.

Ví dụ:

- Lực hấp dẫn giữa Mặt Trời và các hành tinh giữ cho các hành tinh chuyển động quanh Mặt Trời.

- Lực hấp dẫn là lực tác dụng từ xa, qua khoảng không gian giữa các vật.

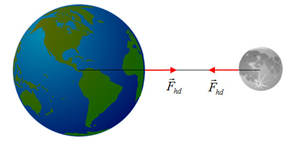
II. Định luật vạn vật hấp dẫn.

Định luật: Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

\({F_{h{\rm{d}}}} = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\)

Trong đó:

  + \(G = 6,67.10^{-11} Nm^2/kg^2\) là hằng số hấp dẫn.

  + m₁, m₂ là khối lượng của hai vật.

  + r là khoảng cách giữa hai tâm của hai vật.

III. Trọng lực là trường hợp riêng của lực hấp dẫn.

- Trọng lực tác dụng lên một vật là lực hấp dẫn giữa Trái Đất và vật đó.

- Trọng lực đặt vào một điểm đặc biệt của vật, gọi là trọng tâm của vật.

- Độ lớn của trọng lực (trọng lượng):

\(P = G\dfrac{{mM}}{{{{(R + h)}^2}}}\)

- Mà P=mg. Do đó, ta có gia tốc rơi tự do:

\(g = \dfrac{{GM}}{{{{(R + h)}^2}}}\)

Với:

  + M là khối lượng của Trái Đất.

  + R là bán kính Trái Đất 6400km.

  + h là độ cao của vật so với mặt đất.

* Nếu ở gần mặt đất thì (h << R), do đó:

\(g = \dfrac{{GM}}{{{{R}^2}}}\) ≈ 9,8m/s².

1. Lực đàn hồi của lò xo. là lực xuất hiện khi lò xo bị biến dạng đàn hồi và có xu hướng chống lại nguyên nhân gây ra biến dạng.

- Mỗi lò xo có một giới hạn đàn hồi nhất định. Trong giới hạn đó, lò xo còn đàn hồi được. Vượt giới hạn đó, lò xo bị biến dạng dẽo.

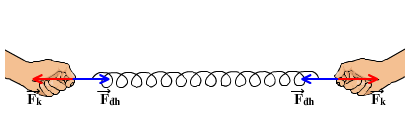
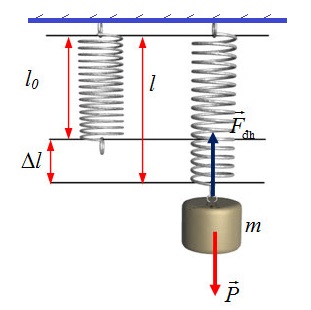
2. Định luật Húc (Hookes): Trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.

\(F_{đh} = k\left| {\Delta l} \right|\)

Trong đó:

  + k là độ cứng (hay hệ số đàn hồi) của lò xo, đơn vị là N/m.

  + Δl là độ biến dạng của lò xo, đơn vị là (m).

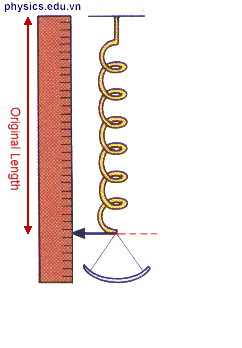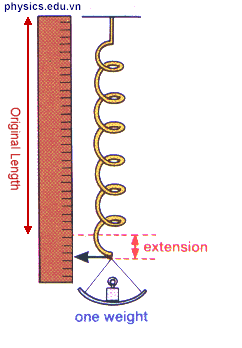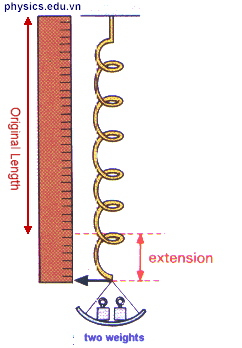
- Lực đàn hồi gồm có:

  + Điểm đặt: tại điểm tiếp xúc với ngoại lực.

  + Phương: trùng với trục lò xo.

  + Chiều: ngược chiều với ngoại lực.

  + Độ lớn: \(F_{đh} = k\left| {\Delta l} \right|\).

3. Chú ý:

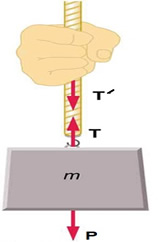
- Đối với dây cao su hay dây thép, lực đàn hồi chỉ xuất hiện khi bị ngoại lực kéo dãn. Vì thế lực đàn hồi trong trường hợp này gọi là lực căng.

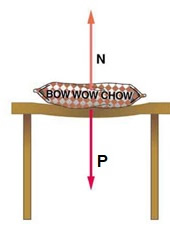
- Đối với mặt tiếp xúc bị biến dạn khi bị ép vào nhau thì lực đàn hồi có phương vuông góc với mặt tiếp xúc.

I. Lực ma sát trượt:

1. Định nghĩa: Lực ma sát trượt là lực suất hiện ở mặt tiếp xúc khi vật này trượt trên vật khác.

- Công thức:

\(F_{mst} = \mu_t N\)

Trong đó:

  + μ_t là hệ số ma sát trượt, phụ thuộc vào vật liệu và tình trạng của hai mặt tiếp xúc.

  + N là áp lực mà vật đè vuông góc lên mặt đỡ.

2. Cách xác định độ lớn của ma sát trượt: Móc lực kế vào vật rồi kéo theo phương ngang cho vật trượt gần như thẳng đều. Khi đó, lực kế chỉ độ lớn của lực ma sát trượt tác dụng vào vật.

3. Đặc điểm của độ lớn của ma sát trượt.

- Có hướng ngược với hướng vận tốc.

- Không phụ thuộc vào diện tích tiếp xúc và tốc độ của vật.

- Tỉ lệ với độ lớn của áp lực.

- Phụ thuộc vào vật liệu và tình trạng của hai mặt tiếp xúc.

II. Lực ma sát lăn.

- Lực ma sát lăn xuất hiện khi một vật lăn trên một vật khác, để cản lại chuyển động lăn của vật.

- Lực ma sát lăn rất nhỏ so với lực ma sát trượt.

III. Lực Ma sát nghĩ.

1. Định nghĩa: Khi tác dụng vào vật một lực, nhưng vật chưa chuyển động, thì mặt tiếp xúc đã tác dụng vào vật một lực, lực đó gọi là lực ma sát nghĩ.

2. Những đặc điểm của lực ma sát nghĩ:

- Lực ma sát nghĩ có hướng ngược với hướng của lực tác dụng song song với mặt tiếp xúc, có độ lớn bằng độ lớn của lực tác dụng, khi vật còn chưa chuyển động.

- Lực ma sát nghĩ có một giá trị cực đại đúng bằng ngoại lực tác dụng song song với mặt tiếp xúc khi vật bắt đầu trượt.

- Khi vật trượt, lực ma sát trượt nhỏ hơn ma sát nghĩ cực đại.

3. Vai trò của lực ma sát nghĩ.

- Nhờ có ma sát nghĩ ta mới cầm nắm được các vật trên tay, đinh mới được giữ lại ở tường, sợi mới kết được thành vải.

- Nhờ có ma sát nghĩ mà dây cua roa chuyển động, băng chuyền chuyển được các vật từ nơi này đến nơi khác.

- Đối với người, động vật, xe cộ, lực ma sát nghĩ đóng vai trò lực phát động.

I. Lực hướng tâm.

1. Định nghĩa: Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.

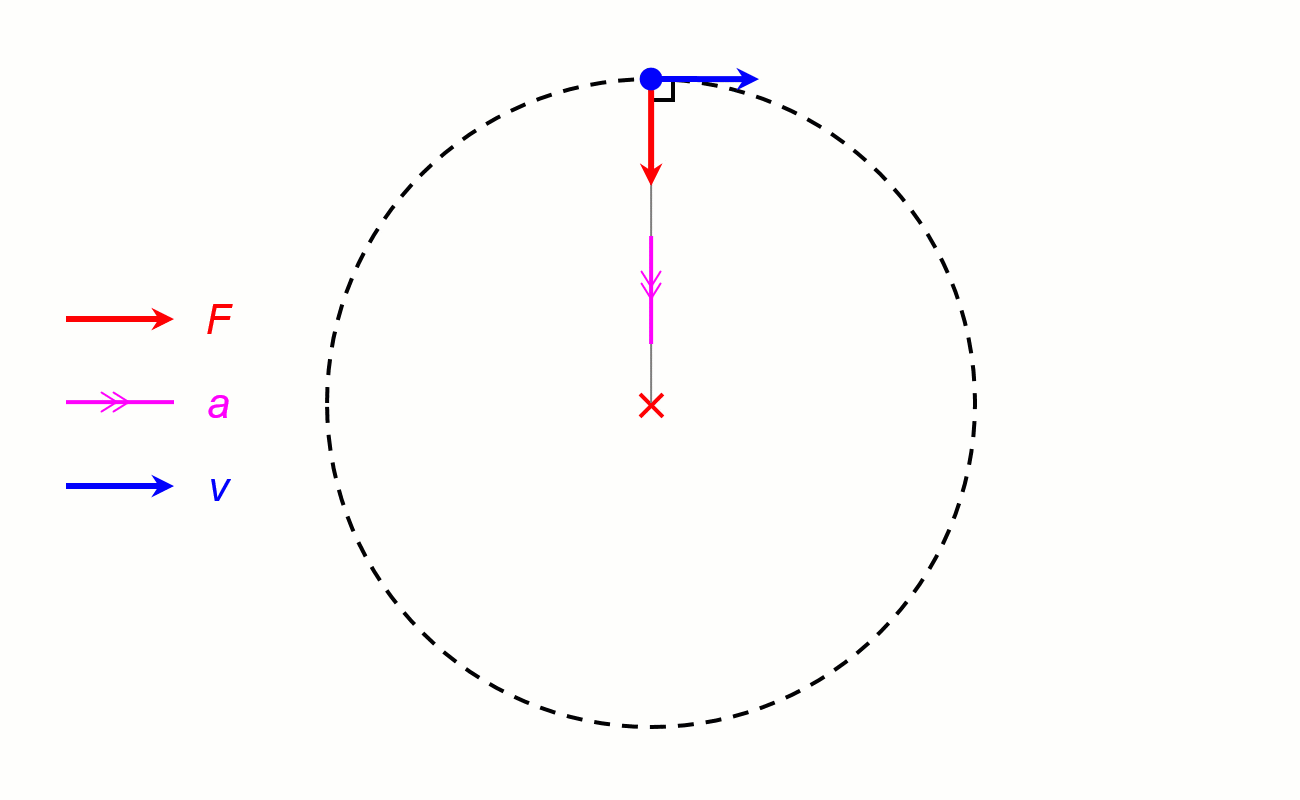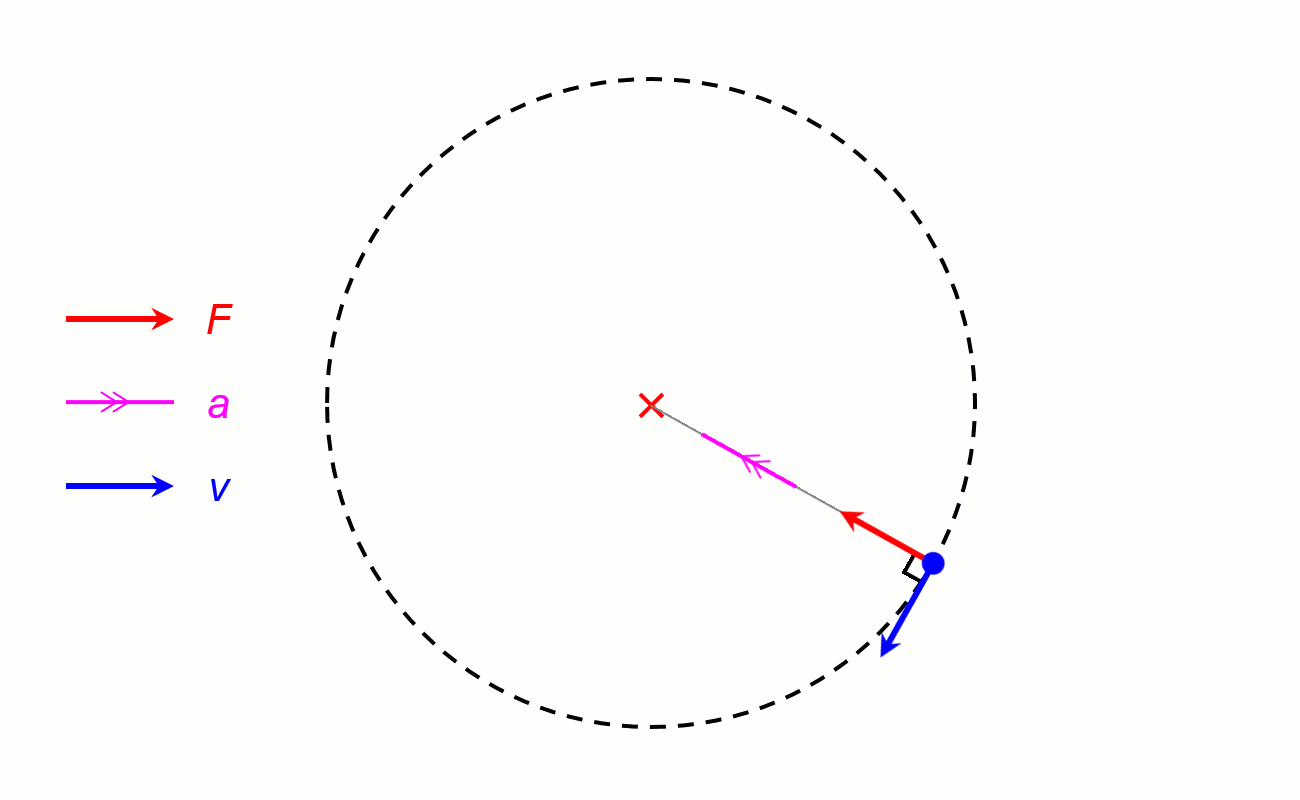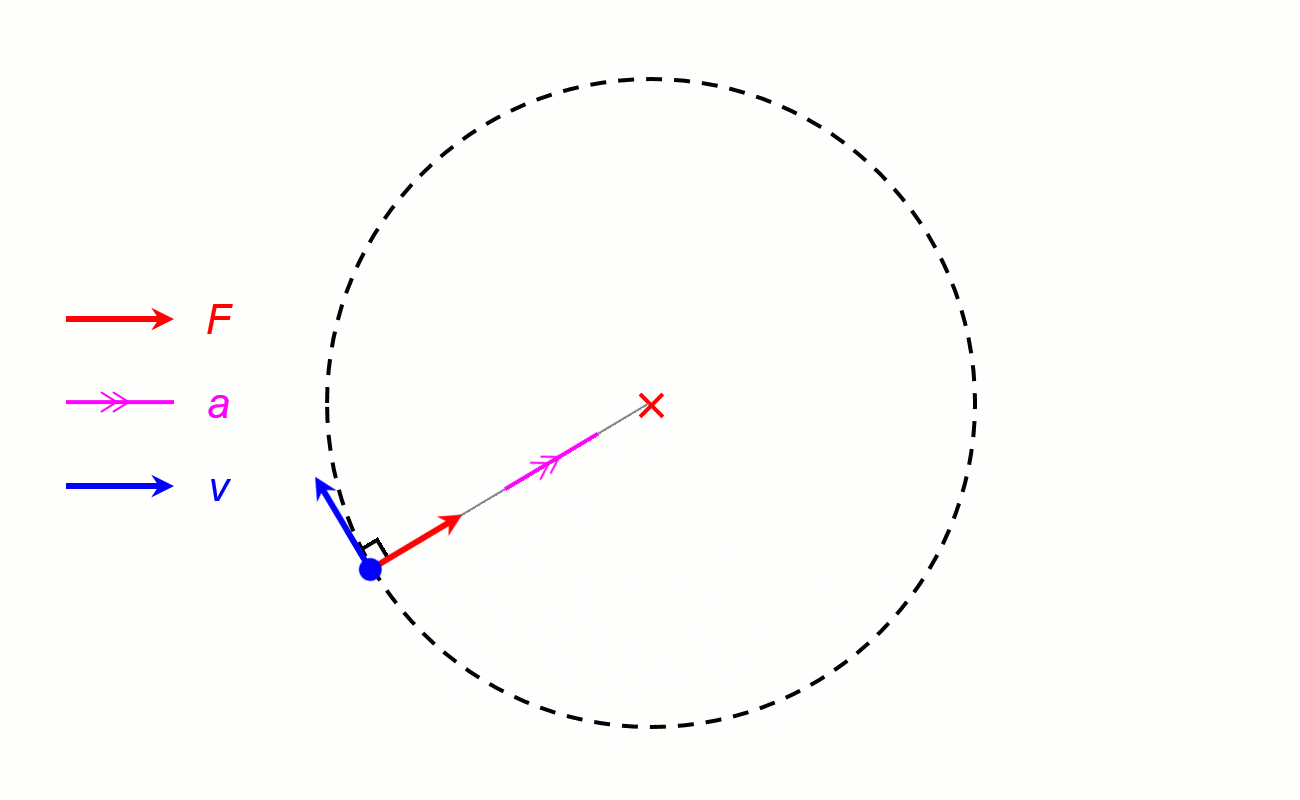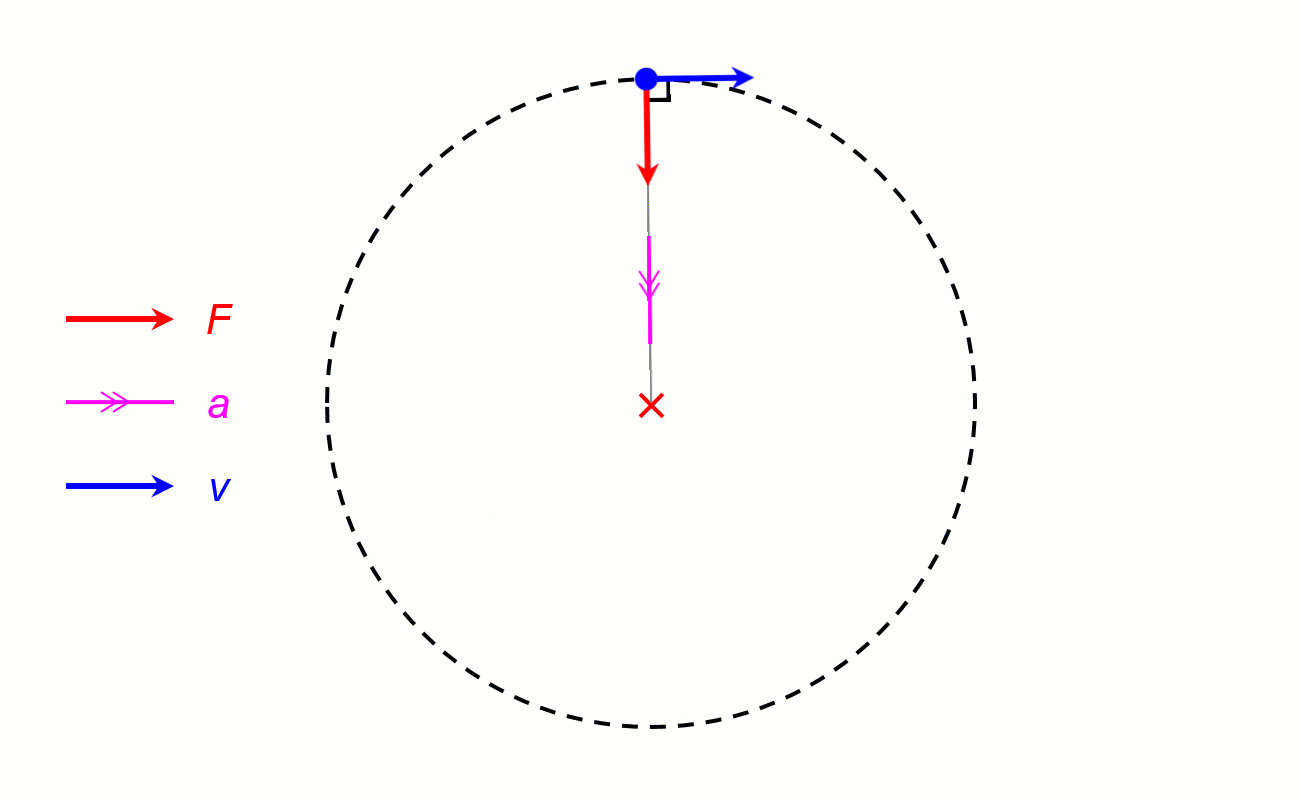
2. Công thức.

\({F_{ht}} = m{a_{ht}} = \frac{{m{v^2}}}{r} = m.{\omega ^2}r\)

Trong đó:

  + F_ht là lực hướng tâm (N).

  + a_ht là gia tốc hướng tâm (m/s²).

  + m là khối lượng của vật (kg).

  + r là bán kính quỹ đạo tròn (m).

  + v là tốc độ dài của vật chuyển động tròn đều (m/s).

  + \(\omega \) là tốc độ góc của vật chuyển động tròn đều (rad/s).

3. Ví dụ.

- Lực hấp dẫn giữa Trái Đất và vệ tinh nhân tạo đóng vai trò lực hướng tâm, giữ cho vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất.

- Đặt một vật trên bàn quay, lực ma sát nghĩ đóng vai trò lực hướng tâm giữ cho vật chuyển động tròn.

- Đường ôtô và đường sắt ở những đoạn cong phải làm nghiên về phía tâm cong để hợp lực giữa trọng lực và phản lực của mặt đường tạo ra lực hướng tâm giữ cho xe, tàu chuyển động dễ dàng trên quỹ đạo.

II. Chuyển động li tâm.

- Khi đặt vật trên bàn quay, nếu bàn quay nhanh quá, lực ma sát nghĩ không đủ lớn để đóng vai trò lực hướng tâm nữa, nên vật trượt trên bàn ra xa tâm quay, rồi văng khỏi bàn theo phương tiếp tuyến với quỹ đạo. Chuyển động như vậy của vật được gọi là chuyển động li tâm.

- Chuyển động li tâm có nhiều ứng dụng thực tế. Ví dụ : Máy vắt li tâm.

- Chuyển động li tâm cũng có khi cần phải tránh. Ví dụ : Khi chạy xe qua những chổ rẽ, chổ quanh, nếu chạy với tốc độ lớn thì lực ma sát nghĩ cực đại không đủ lớn để đóng vai trò lực hướng tâm giữ cho xe chuyển động tròn nên xe sẽ trượt li tâm, dễ gây ra tai nạn giao thông.

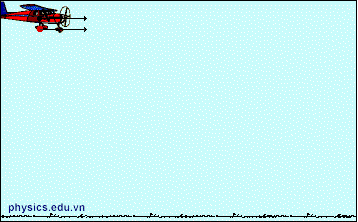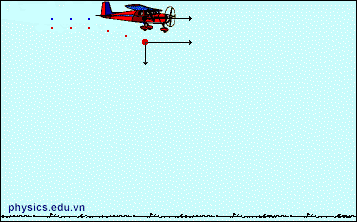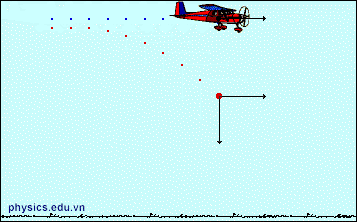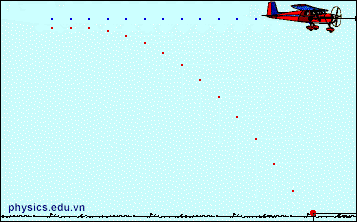
I. Khảo sát chuyển động của vật ném ngang.

1. Định nghĩa: Là chuyển động ném theo phương ngang từ độ cao h, với vận tốc \(\overrightarrow {{v_0}} \) của vật song song với mặt đất.

2. Chọn hệ trục toạ độ và gốc thời gian.

- Chọn hệ trục toạ độ Decart Oxy với trục Ox hướng theo véctơ vận tốc \(\overrightarrow {{v_0}} \), trục Oy hướng theo véctơ trọng lực \(\overrightarrow {{p}} \).

- Chọn gốc thời gian lúc bắt đầu ném.

3. Phân tích chuyển động ném ngang.

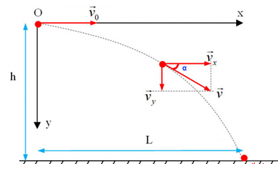
- Chuyển động của các hình chiếu M_x và M_y trên các trục Ox và Oy gọi là các chuyển động thành phần của vật M.

Trên trục Ox.	Trên trục Oy.
- Gia tốc: ax = 0. - Vận tốc: vx = v0. - Hoành độ: x = v0t.	- Gia tốc: ay = g. - Vận tốc: vy = gt. - Tung độ: y = \(\frac{1}{2}gt^2\).
- Phương trình quỹ đạo. y = \(\frac{g}{2v_0^2}x^2\) - Phương trình vận tốc. \(v = \sqrt {(gt)^2 + v_0^2} \) - Thời gian chuyển động đến khi chạm đất. \(t = \sqrt {\dfrac{{2h}}{g}} \) - Tầm ném xa. \(L = {v_0}t = {v_0}\sqrt {\dfrac{{2h}}{g}} \)

II. Thí nghiệm kiểm chứng.

- Sau khi búa đập vào thanh thép, bi A chuyển động ném ngang còn bi B rơi tự do. Cả hai đều chạm đất cùng một lúc.

III. Ứng dụng.